02. Терминология и классификация игр

В теории игр предполагается, что игра состоит из Ходов, выполняемых игроками одновременно или последовательно.

Ходы бывают Личными и Случайными. Ход называется Личным, если игрок сознательно выбирает его из совокупности возможных вариантов действий и осуществляет его (например, любой ход в шахматной игре). Ход называется Случайным, если его выбор производится не игроком, а каким-либо механизмом случайного выбора (например, по результатам бросания монеты).

Совокупность ходов, предпринятых игроками от начала до окончания игры, называется Партией.

Одним из основных понятий теории игр является понятие стратегии. Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от ситуации, сложившейся в процессе игры. В простых (одноходовых) играх, когда в каждой партии игрок может сделать лишь по одному ходу, понятие стратегии и возможного варианта действий совпадают. В этом случае совокупность стратегий игрока охватывает все возможные его действия, а любое возможное для игрока I действие является его стратегией. В сложных (многоходовых играх) понятие «варианта возможных действий» и «стратегии» может отличаться друг от друга.

Стратегия игрока называется оптимальной, если она обеспечивает данному игроку при многократном повторении игры максимально возможный средний выигрыш или минимально возможный средний проигрыш, независимо от того, какие стратегии применяет противник. Могут быть использованы и другие критерии оптимальности.

Возможно, что стратегия, обеспечивающая максимальный выигрыш, не обладает другим важным представлением оптимальности, как устойчивостью (равновесностью) решения. Решение игры является устойчивым (равновесным), если соответствующие этому решению стратегии образуют ситуацию, которую ни один из игроков не заинтересован изменить.

Повторим, что задача теории игр - нахождение оптимальных стратегий.

Классификация игр представлена на рис. 1.1.

1. В зависимости От видов ходов игры подразделяются на стратегические и азартные. Азартные игры состоят только из случайных ходов - ими теория игр не занимается. Если наряду со случайными ходами есть личные ходы, или все ходы личные, то такие игры называются Стратегическими.

2. В зависимости От числа участников игры подразделяются на парные и множественные. В парной игре число участников равно двум, В множественной - более двух.

3. Участники множественной игры могут образовывать коалиции, как постоянные, так и временные. По характеру взаимоотношений игроков игры делятся на бескоалиционные, коалиционные и кооперативные.

Бескоалиционными называются игры, в которых игроки не имеют право вступать в соглашения, образовывать коалиции, и целью каждого игрока является получение по возможности наибольшего индивидуального выигрыша.

Игры, в которых действия игроков направлены на максимизацию выигрышей коллективов (коалиций) без последующего их разделения между игроками, называются Коалиционными.

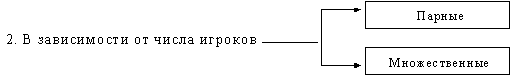
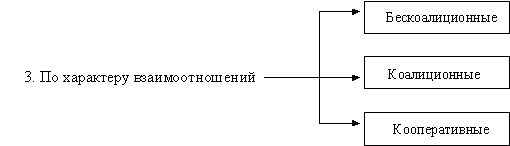
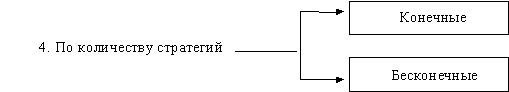
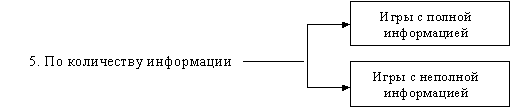
Рис. 1.1. Классификация игр

Исходом Кооперативной игры является дележ выигрыша коалиции, который возникает не как следствие тех или иных действий игроков, а как результат их наперед определенных соглашений.

В соответствии с этим в кооперативных играх сравниваются по предпочтительности не ситуации, как это имеет место в бескоалиционных играх, а дележи; и сравнение это не ограничивается рассмотрением индивидуальных выигрышей, а носит более сложный характер.

4. По количеству стратегий каждого игрока игры подразделяются на конечные (число стратегий каждого игрока конечно) и Бесконечные (множество стратегий каждого игрока бесконечно).

5. По количеству информации, имеющейся у игроков относительно прошлых ходов, игры подразделяются на игры с Полной информацией (имеется вся информация о предыдущих ходах) и Неполной информацией. Примерами игр с полной информацией могут быть шахматы, шашки и т. п.

6. По виду описания игры подразделяются на позиционные игры (или игры в развернутой форме) и игры в нормальной форме. Позиционные игры задаются в виде дерева игры. Но любая позиционная игра может быть сведена К нормальной форме, в которой каждый из игроков делает только по одному независимому ходу. В позиционных играх ходы делаются в дискретные моменты времени. Существуют Дифференциальные игры, в которых ходы делаются непрерывно. Эти игры изучают задачи преследования управляемого объекта другим управляемым объектом с учетом динамики их поведения, которая описывается дифференциальными уравнениями.

Существуют также Рефлексивные игры, которые рассматривают ситуации с учетом мысленного воспроизведения возможного образа действий и поведения противника.

7. Если любая возможная партия некоторой игры имеет нулевую сумму выигрышей FI, всех N игроков (), то говорят об игре С нулевой суммой. В противном случае игры называются играми С ненулевой суммой.

Очевидно, что парная игра с нулевой суммой является Антагонистической, так как выигрыш одного игрока равен проигрышу второго, а следовательно цели этих игроков прямо противоположны.

Конечная парная игра с нулевой суммой называется Матричной игрой. Такая игра описывается платежной матрицей, в которой задаются выигрыши первого игрока. Номер строки матрицы соответвует номеру применяемой стратегии первого игрока, столбец - номеру применяемой стратегии второго игрока; на пересечении строки и столбца находится соответствующий выигрыш первого игрока (проигрыш второго игрока).

Конечная парная игра с ненулевой суммой называется Биматричной игрой. Такая игра описывается двумя платежными матрицами, каждая для соответствующего игрока.

< Предыдущая		Следующая >