1.3.7. Статистические игры

Принятие решений в условиях неопределенности.

Одним из определяющих факторов в таких задачах является внешняя среда или природа, которая может находиться в одном из состояний S1, … ,Sк, которые неизвестны лицу(наблюдателю) принимающему решения.

Тогда математическую модель задачи в условиях неопределенности можно сформулировать следующим образом.

Имеется некоторая матрица L размерностью m ´ n с элементами, рассматриваемыми как полезность результата 0j при использовании стратегии xi

Lij = U(0j, xi), j=1…n, I=1..m.

Xi\0j	01	02	…..	0m
X1	L11	L12	…..	L1m
x1	L21	L22	……	L2m
……	…..	…..	……
xn	Ln1	Ln2	……	Lnm

В зависимости от состояния среды результат 0j достигается с вероятностью Р(0j/xi, Sk).

Кроме того, наблюдателю неизвестно распределение вероятностей Р(Sk). Относительно состояния среды наблюдатель может высказать определенные гипотезы.

Его предположения о вероятном состоянии среды называются субъективными вероятностями `Р(Sk), к=1..к.

Если бы величина Р(Sk) была известна наблюдателю, то мы бы имели задачу принятия решений в условиях риска, и в этом случае решающее правило для определения стратегии определялось бы следующим образом

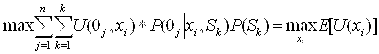(1)

На самом деле же состояния среды неизвестны и неизвестно также распределения вероятностей Р(Sk) .

Как поступить в данном случае?

Существует несколько критериев для выбора оптимальной стратегии.
Критерий Вальда (критерий осторожного наблюдателя). Этот критерий оптимизирует полезность в предположении, что среда находится в самом невыгодным для наблюдателя состоянии : по заданному критерию решающее правило имеет следующий вид :

(2), где

,i=1...m, k=1…k

По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния среды.

Критерий Гурвица. Основан на следующих двух предложениях : среда может находиться в самом невыгодном состоянии с вероятностью 1-a и в самом выгодном с вероятностью a, где a-коэффициент доверия. Тогда решающее правило записывается так:

(3)

Если a=0, то получаем критерий Вальда.

Если a=1,то приходим к решающему правилу вида: (4) – так называемая стратегия “здорового оптимиста”, который верит в удачу.

Критерий Лапласа. Если неизвестны состояния среды, то все состояния среды считаются равновероятными:

В результате решающее правило определяется соотношением (1) при условии Р(Sk)=1/k.

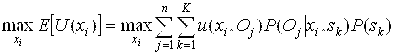(5), при условии, что

Критерий Сэвиджа. (критерий минимизации “сожалений”).

“Сожаление “ – это величина, равная изменению полезности результата при данном состоянии среды относительно наилучшего возможного состояния.

Чтобы определить “сожаление” поступают следующим образом. Строят матрицу U = ||uik || где uik = u(xi, sk), 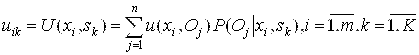. В каждом столбце этой матрицы находится максимальный элемент

Его вычитают из всех элементов этого столбца. Далее строим матрицу сожалений

. Искомую стратегию хi , которая минимизирует “сожаление”, определяют из условия

(6)

Этот критерий минимизирует возможные потери при условии, что состояние среды наихудшем образом отличается от предлагаемого.

Рассмотрим частный случай модели задачи в условиях неопределенности.

Предположим, что каждому возможному состоянию среды соответствует один возможный исход :

, где

Т. о., в данном случае мат. модель задачи принятия решений определяется множеством стратегий x = {xi}, множеством состояний среды s={sk}, а также матрицей полезностей

Xi/ S	S1	S2	….	Sk
x1	L11			L1k
x2
….
Xn	Ln1			Lnk

Где Lij= U(xi, sj ).

Множество {P(sj)} предполагается неизвестным.

В этом случае критерий для выбора оптимальной стратегии имеет следующий вид:

Критерий Вальда:

Критерий Гурвица:

Критерий Лапласа:

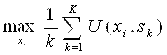
Критерий Сэвиджа:

, где

Пример Использования данных критериев в условиях неопределенности.

Некоторая фирма решает построить отель в одном из курортных мест. Необходимо определить наиболее целесообразное количество мест или комнат в этой гостинице.

Составляют смету расходов по строительству гостиницы с различным количеством комнат, а также рассчитывают ожидаемый доход в зависимости от количества комнат, которые будут сняты.

В зависимости от принятого решения –количество комнат в гостинице х = 20, 30,40,50 и количества снятых комнат s = 0, 10, 20, 30, 40, 50, которое зависит от множества случайных факторов и заранее неизвестно туристической фирме, получают следующую таблицу ежегодных прибылей

Xi/sk	0	10	20	30	40	50
20	-121	62	245	245	245	245
30	-168	14	198	380	380	380
40	-216	-33	150	332	515	515
50	-264	-81	101	284	468	650

Наиболее подходящее количество комнат в гостинице определяют по рассмотренным критериям.

Критерий Вальда:

, xопт=20.

Судя по результату, критерий Вальда неприменим, т.к. в этом случае от постройки гостиницы следует отказаться.

Критерий Лапласа:

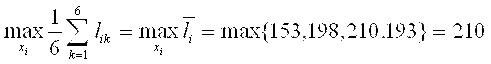
Т. е. -среднее арифметическое по каждой строке таблицы.

Xопт=20.

Критерий Гурвица:

Для разных a можно построить таблицу доходов по критерию Гурвица Н=||hij||, где

Xi/	0.1	0.2	0.5	0.9
20	-84	-47	63	206
30	-114	-59	108	325
40	-143	-70	150	442
50	-172	-81	193	560

Для i = 1

Тогда оптимальное количество места в гостинице в зависимости от a: можно записать следующей таблицей

	0.1	0.2	0.5	0.9
Xопт	20	20	50	50

Т. о. 20 комнат, если заказчик пессимист, 50-если оптимист.

Критерий Сэвиджа:

Строят матрицу сожалений:

Xi/si	0	10	20	30	40	50
20	0	0	0	-135	-270	-405
30	-47	-48	-47	0	-135	-275
40	-95	-95	-95	-48	0	-135
50	-145	-143	-144	-96	-47	0

Т. о. xопт=40.

Какое из решений предпочтительнее, определяется выбором критерия.

Выбор критерия принятия решения является наиболее сложным и ответственным этапом в исследовании операций. При этом не существует каких-либо общих рекомендаций или советов. Выбор критерия должен производить заказчик на самм высоком уровне и в максимальной степени согласовывать этот выбор с конкретной спецификацией задачи, а также со своими целями.

В частности, если даже минимальный риск недопустим, то следует применять критерий Вальда. Если наоборот, определенный риск вполне приемлем и заказчик намерен вложить в некоторое предприятие столько средств, чтобы потом он не сожалел, что вложил слишком мало, то выбирают критерий Сэвиджа.

При отсутствии достаточной информации для выбора того или иного критерия возможен альтернативный подход, который может быть связан с вычислением шансов на успех или неуспех на основе прошлого опыта.

Принятие решений в условиях конфликтных ситуаций или противодействия.

В отличие от задач принятия решений в условиях определенности, риска и неопределенности, в которых внешняя среда (природа) предполагалась пассивной, Конфликтные ситуации Предполагают наличие по крайней мере двух противодействующих сторон, интересы которых противоположны. Упрощенная математическая модель конфликтных ситуаций представляет собой игру.

Игра может быть определена следующим образом:

Имеются n конфликтных сторон (лиц) принимающих решения, интересы которых совпадают.

Заданы правила, определяющие выбор допустимых стратегий, известные игрокам.

Существует точно определенный набор конечных состояний, которым заканчивается игра (например, выигрыш, ничья, проигрыш).

Заранее определены и известны всем игрокам платежи, соответствующие каждому возможному конечному состоянию. Обычно они заданы в виде некоторой матрицы А = || аij|| .

Практические задачи, в которых встречаются игровые аспекты, чрезвычайно разнообразны.

Характерным примером является довольно распространенная ситуация, когда несколько фирм добиваются права у заказчика на получение выгодного заказа или конфликтуют из-за обладания новыми рынками сбыта.

< Предыдущая		Следующая >