1.4.1. Определение бесконечной антагонистической игры
Естественным обобщением матричных игр являются бесконечные антагонистические игры (БАИ), в которых хотя бы один из игроков имеет бесконечное количество возможных стратегий. Мы будем рассматривать игры двух игроков, делающих по одному ходу, и после этого происходит распределение выигрышей. При формализации реальной ситуации с бесконечным числом выборов можно каждую стратегию сопоставить определённому числу из единичного интервала, т. к. всегда можно простым преобразованием любой интервал перевести в единичный и наоборот.
Напоминание. Пусть Е – некоторое множество вещественных чисел. Если существует число Y, такое, что X £ Y при всех ХÎЕ (при этом Y не обязательно принадлежит Е), то множество Е называется ограниченным сверху, а число Y называется верхней границей множества Е. Аналогично определяется ограниченность снизу и нижняя граница множества Е. Обозначаются верхняя и нижняя границы соответственно через sup Е и inf Е соответственно.
Пример. Пусть множество Е состоит из всех чисел вида ![]() , N = 1,2, ... Тогда множество Е ограничено, его верхняя грань равна 1, а нижняя 0, причём 0ÏЕ , а 1ÎЕ.
, N = 1,2, ... Тогда множество Е ограничено, его верхняя грань равна 1, а нижняя 0, причём 0ÏЕ , а 1ÎЕ.
Для дальнейшего изложения теории игр этого класса введём определения и обозначения : [0; 1] – единичный промежуток, из которого игрок может сделать выбор; Х – число (стратегия), выбираемое игроком 1; Y – число (стратегия), выбираемое игроком 2; МI(X,Y) – выигрыш I-го игрока; G (X,Y,M1,M2) – игра двух игроков, с ненулевой суммой, в которой игрок 1 выбирает число Х из множества Х, игрок 2 выбирает число Y из множества Y, и после этого игроки 1 и 2 получают соответственно выигрыши M1(X, Y) и M2(X, Y). Пусть, далее, G (X,Y,M) – игра двух игроков с нулевой суммой, в которой игрок 1 выбирает число Х, игрок 2 – число Y, после чего игрок 1 получает выигрыш М(X, Y) за счёт второго игрока.
Большое значение в теории БАИ имеет вид функции выигрышей M(X, Y). Так, в отличии от матричных игр, не для всякой функции M(X, Y) существует решение. Будем считать, что выбор определённого числа игроком означает применение его чистой стратегии, соответствующей этому числу. По аналогии с матричными играми назовём чистой нижней ценой игры величину
V1 = ![]()
![]() M(x, y) или V1 =
M(x, y) или V1 = ![]()
![]() M(x, y),
M(x, y),
А чистой верхней ценой игры величину
V2 = ![]()
![]() M(x, y) или V2 =
M(x, y) или V2 = ![]()
![]() M(x, y),
M(x, y),
Для матричных игр величины V1 и V2 всегда существуют, а в бесконечных играх они могут и не существовать.
Естественно считать, что, если для какой-либо бесконечной игры величины V1 и V2 существуют и равны между собой (V1 = V2 = V), то такая игра имеет решение в чистых стратегиях, т. е. оптимальной стратегией игрока 1 есть выбор числа XoÎX и игрока 2 – числа YoÎY, при которых M(Xo, Yo) = V, в этом случае V называется ценой игры, а (xO, Yo) – седловой точкой в чистых стратегиях.
Пример 1. Игрок 1 выбирает число Х из множества Х = [0; 1], игрок 2 выбирает число Y из множества Y = [0; 1]. После этого игрок 2 платит игроку 1 сумму
M(x, y) = 2х2 - y2.
Поскольку игрок 2 хочет минимизировать выигрыш игрока 1, то он определяет
![]() (2x2 - y2) = 2х2 - 1,
(2x2 - y2) = 2х2 - 1,
Т. е. при этом y = 1. Игрок 1 желает максимизировать свой выигрыш, и поэтому определяет
![]() (
(![]() M(x, y)) =
M(x, y)) = ![]() (2х2 - 1) = 2-1 = 1,
(2х2 - 1) = 2-1 = 1,
Который достигается при Х = 1.
Итак, нижняя цена игры равна V1 = 1. Верхняя цена игры
V2 = ![]() (
(![]() (2х2 - y2)) =
(2х2 - y2)) = ![]() (2 - y2) = 2-1 = 1,
(2 - y2) = 2-1 = 1,
Т. е. в этой игре V1 = V2 = 1. Поэтому цена игры V = 1, а седловая точка (1;1).
Пример 2. Игрок 1 выбирает ХÎX = (0; 1), игрок 2 выбирает YÎY = (0; 1). После этого игрок 1 получает сумму
M(x, y) = x + y
За счёт игрока 2. Поскольку Х и Y - открытые интервалы, то на них V1 И V2 не существуют. Если бы Х и Y Были замкнутые интервалы, то, очевидно, было бы следующее :
V1 = V2 = 1 при xo = 1, yo = 0.
С другой стороны, ясно, что, выбирая х достаточно близкое к 1, игрок 1 будет уверен, что он получит выигрыш не меньше, чем число, близкое к цене игры V = 1; выбирая Y близкое к нулю, игрок 2 не допустит, чтобы выигрыш игрока 1 значительно отличался от цены игры V = 1.
Степень близости к цене игры может характеризоваться числом e > 0. Поэтому в описываемой игре можно говорить об оптимальности чистых стратегий ХO = 1, YO = 0 соответственно игроков 1 и 2 с точностью до произвольного числа e > 0. В связи с этим введём следующие определения.
Точка (![]() ,
,![]() ), где
), где ![]() ÎX,
ÎX, ![]() ÎY, в антагонистической непрерывной игре G называется точкой e-равновесия, если для любых стратегий XÎX игрока 1, yÎY игрока 2 имеет место неравенство
ÎY, в антагонистической непрерывной игре G называется точкой e-равновесия, если для любых стратегий XÎX игрока 1, yÎY игрока 2 имеет место неравенство
М(х,![]() ) - e £ M(
) - e £ M(![]() ,
,![]() ) £ М(
) £ М(![]() , y) + e.
, y) + e.
Точка e-равновесия (![]() ,
,![]() ) называется также e-седловой точкой функции М(X, y), а стратегии
) называется также e-седловой точкой функции М(X, y), а стратегии ![]() и
и ![]() называются e-оптимальными стратегиями. Эти стратегии являются оптимальными с точностью до e в том смысле, что, если отклонение от оптимальной стратегии никакой пользы игроку принести не может, то его отклонение от e-оптимальной стратегии может увеличить его выигрыш не более, чем на e.
называются e-оптимальными стратегиями. Эти стратегии являются оптимальными с точностью до e в том смысле, что, если отклонение от оптимальной стратегии никакой пользы игроку принести не может, то его отклонение от e-оптимальной стратегии может увеличить его выигрыш не более, чем на e.
Можно доказать, что для того, чтобы функция М имела e-седловые точки для любого e > 0 необходимо и достаточно чтобы
![]()
![]() M(x, y) =
M(x, y) = ![]()
![]() M(x, y).
M(x, y).
Если игра G не имеет седловой точки (e-седловой точки) в чистых стратегиях, то оптимальные стратегии можно искать среди смешанных стратегий. Однако, в качестве вероятностной меры здесь вводятся функции распределения вероятностей применения игроками чистых стратегий.
Пусть F(Х) – функция распределения вероятностей применения чистых стратегий игроком 1. Если число x - чистая стратегия игрока 1, то
F(х) = P(x £ х),
Где P(x £ Х) означает вероятность того, что случайно выбранная чистая стратегия x не будет превосходить числа Х. Аналогично рассматривается функция распределения вероятностей применения чистых стратегий h игроком 2
Q(y) = P(h £ y).
Функции F(Х) и Q(Y) называются смешанными стратегиями соответственно игроков 1 и 2. Если F(Х) и Q(Y) дифференцируемы, то существуют их производные, обозначаемые соответственно через F(X) и Q(Y) (функции плотности распределения).
В общем случае дифференциал функции распределения DF(Х) выражает вероятность того, что стратегия x находится в промежутке
х £ x £ х + dх.
Аналогично для игрока 2: DQ(Y) означает вероятность того, что его стратегия h находится в интервале
y £ h £ y + dy.
Тогда выигрыш игрока 1 составит
М(х, y) dF(х),
А выигрыш игрока 2 равен
М(х, y) dQ(y).
Средний выигрыш игрока 1 при условии, что игрок 2 применяет свою чистую стратегию Y, получим, если проинтегрируем выигрыш по всем возможным значениям Х, т. е.
E(F, y) = 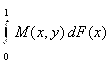
Напомним, что множество Y для y является замкнутым промежутком [0; 1].
Если игрок 1 применяет свою чистую стратегию Х, а игрок 2 - Y, то выигрыш игрока 1 составит
М(х, y) dP(х) dQ(y).
Средний выигрыш игрока 1 при условии, что оба игрока применяют свои смешанные стратегии F(Х) и Q(Y), будет равен
E(F, Q) = 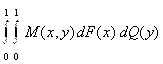 .
.
По аналогии с матричными играми определяются оптимальные смешанные стратегии игроков и цена игры: в антагонистической непрерывной игре G(Х, Y,М) пара смешанных стратегий F*(Х) и Q*(Y) соответственно для игроков 1 и 2 образует седловую точку в смешанных стратегиях, если для любых смешанных стратегий F(Х) и Q(Y) справедливы соотношения
Е(F, Q*) £ Е(F*,Q*) £ Е (F*,Q).
Из левой части последнего неравенства следует, что если игрок 1 отступает от своей стратегии F*(Х), то его средний выигрыш не может увеличиться, но может уменьшиться за счёт лучших действий игрока 2, поэтому F*(Х) называется оптимальной смешанной стратегией игрока 1.
Из правой части последнего неравенства следует, что если игрок 2 отступит от своей смешанной стратегии Q*(Y), то средний выигрыш игрока 1 может увеличиться, а не уменьшиться, за счёт более разумных действий игрока 1, поэтому Q*(Y) называется оптимальной смешанной стратегией игрока 2. Средний выигрыш Е(F*,Q*), получаемый игроком 1 при применении игроками оптимальных смешанных стратегий, называется ценой игры.
По аналогии с матричными играми рассматривается нижняя цена непрерывной игры в смешанных стратегиях
V1 = ![]()
![]() E(F, Q)
E(F, Q)
И верхняя цена игры
V2 = ![]()
![]() E(F, Q).
E(F, Q).
Если существуют такие смешанные стратегии F*(Х) и Q*(Y) соответственно для игроков 1 и 2, при которых нижняя и верхняя цены непрерывной игры совпадают, то F*(Х) и Q*(Y) естественно назвать оптимальными смешанными стратегиями соответствующих игроков, а V1 = V2 = V – ценой игры.
Можно доказать, что существование седловой точки в смешанных стратегиях игры G(Х, Y,М) равносильно существованию верхней V2 и нижней V1 цен игры в смешанных стратегиях и их равенству V1 = V2 = V.
Таким образом, решить игру G(Х, Y,М) – означает найти седловую точку или такие смешанные стратегии, при которых нижняя и верхняя цены игры совпадают.
Теорема 1 (существования). Всякая антагонистическая бесконечная игра двух игроков G с непрерывной функцией выигрышей М(Х, y) на единичном квадрате имеет решение (игроки имеют оптимальные смешанные стратегии).
Теорема 2. Пусть – бесконечная антагонистическая игра с непрерывной функцией выигрышей М(Х, Y) на единичном квадрате и ценой игры V. Тогда, если Q(Y) – оптимальная стратегия игрока 2 и для некоторого XO
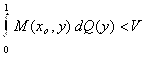 ,
,
То XO Не может входить в точки спектра оптимальной стратегии игрока 1; если F(Х) – оптимальная стратегия игрока 1и для некоторого YO
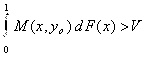 ,
,
То YO не может быть точкой спектра оптимальной стратегии игрока 2.
Из теоремы 2 следует, что если один из игроков применяет оптимальную стратегию, а другой – чистую, притом что средний выигрыш игрока 1 отличается от цены игры, то эта чистая стратегия не может войти в его оптимальную стратегию (или она входит в неё с вероятностью нуль).
Теорема 3. Пусть в бесконечной антагонистической игре функция выигрышей М(Х,Y) непрерывная для ХÎ[0; 1], YÎ[0; 1] и
М(х, y) = - М(y, х),
Тогда цена игры равна нулю и любая оптимальная стратегия одного игрока будет также оптимальной стратегией другого игрока.
Сформулированные свойства оптимальных смешанных стратегий и цены игры помогают находить или проверять решения, но они ещё не дают в общем виде приемлемых методов решения игры. Более того, не существует общих методов для точного нахождения решения БАИ, и в том числе непрерывных игр на единичном квадрате. Поэтому рассматриваются частные виды антагонистических бесконечных игр.
| < Предыдущая | Следующая > |
|---|