2.2. Свойства преобразования Фурье

1.Убывание на бесконечности. Предположим, что и . Интегрируя по частям, имеем

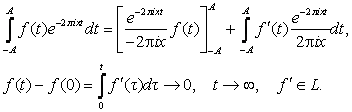
Поэтому

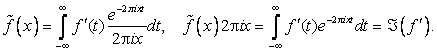
Отсюда (3)

2. Дифференцируемость. Дифференцируя формально, имеем

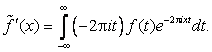
Если 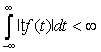, то интеграл для сходится равномерно для , принадлежащих конечным промежуткам и . Вообще, если , то раз дифференцируема и

(4)

3. Класс функций, быстро убывающих вместе со всеми производными. определяется так . Последовательность . Из свойств 1,2 вытекает, что

< Предыдущая		Следующая >