2.3. Примеры

1.

Здесь ограничена, а уже не ограничена.

2. (5)
Имеем по теореме Коши

Для получаем

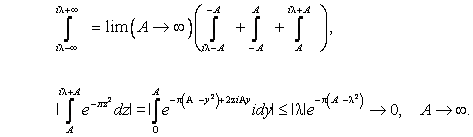
Аналогично, стремится к нулю и третий интеграл. Поэтому окончательно

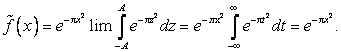
Отсюда следует

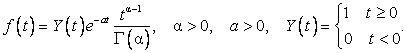
Здесь имеем

Поэтому

.

Аналогично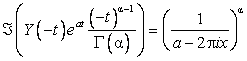

Складывая, получаем

При это дает .

Прямое доказательство последней формулы:

4 Преобразование Фурье рациональной функции, непрерывной на вещественной оси и стремящейся к нулю на бесконечности. Пусть

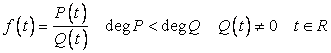, - - нули знаменателя в верхней и нижней полуплоскости. Выбирая подходящую полуокружность и применяя лемму Жордана, получаем

5. В частном случае. ( интеграл Лапласа ) имеем

6. В вырожденном частном случае (интеграл Эйлера) имеем

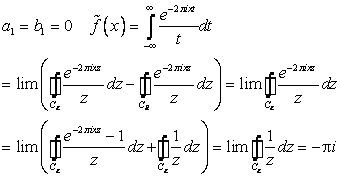
Откуда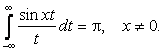

7. Наконец, найдем косинус-преобразование . Так как имеет простые полюсы в верхней полуплоскости в точках , по формуле Коши получаем

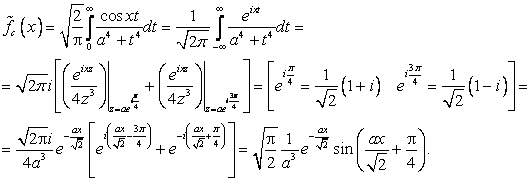
< Предыдущая		Следующая >