2.1. Интегралы Фурье. Преобразование Фурье

Пусть - комплекснозначная функция. Ее преобразованием Фурье называется комплекснозначная функция вещественного переменного

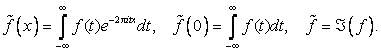(1)

Вместе с определяется обратное преобразование

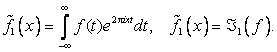
Если функция вещественна, то отделяя в (1) вещественную и мнимую часть и полагая , получаем вещественную форму преобразования Фурье

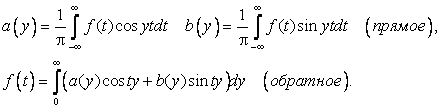(2)

Для четных функций вещественное преобразование Фурье и его обратное может быть записано в симметричной форме с использованием косинус-преобразования Фурье

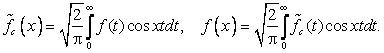
Аналогично, для нечетных функций пара вещественных преобразований Фурье сводится к синус-преобразованию Фурье

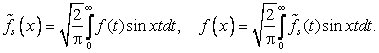
Преобразование определено

1. Для суммируемой ; при этом

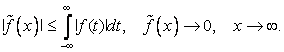(Лебег)

2. Для , монотонно убывающей к нулю на бесконечности (Дирихле).

При этом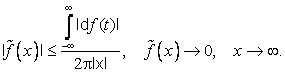

< Предыдущая		Следующая >