1.7. Двойные ряды Фурье
Пусть ![]() – комплекснозначная функция двух переменных, имеющая период
– комплекснозначная функция двух переменных, имеющая период ![]() по
по ![]() ,
, ![]() по
по ![]() и суммируемая в прямоугольнике
и суммируемая в прямоугольнике ![]() . Ей сопоставляется двойной ряд Фурье
. Ей сопоставляется двойной ряд Фурье
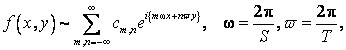 (11)
(11)
Коэффициенты которого определяются по формуле
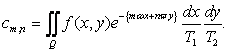
Если ![]() вещественна, удобно пользоваться вещественной формой ряда (11)
вещественна, удобно пользоваться вещественной формой ряда (11)
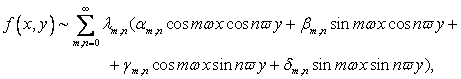
Где 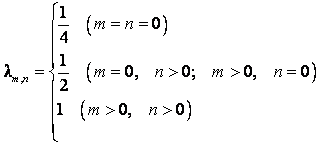
И 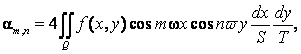
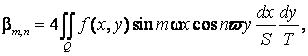
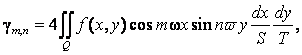

Пусть 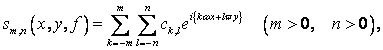
Частная сумма ряда (11) по прямоугольнику ![]() , а
, а 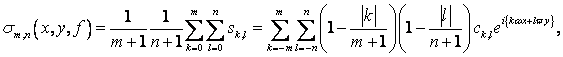
Их среднее арифметическое.
Справедливы следующие утверждения
Теорема 1. Пусть частные производные 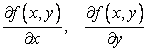 ограничены в
ограничены в ![]() , а смешанная производная
, а смешанная производная 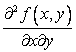 непрерывна в точке
непрерывна в точке ![]() . Тогда
. Тогда ![]()
Теорема 2. Пусть ![]() суммируема в
суммируема в ![]() . Тогда в каждой точке
. Тогда в каждой точке ![]() непрерывности
непрерывности ![]()
Пример. Разложить в двойной ряд Фурье функцию ![]() , в квадрате
, в квадрате ![]()
Принимая во внимание четность (нечетность) подинтегральных функций находим

 ;
;
 ;
;
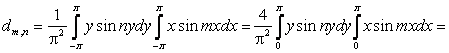

Следовательно, при ![]()
![]()
| < Предыдущая | Следующая > |
|---|