1.6. Суммируемость рядов Фурье

В этом пункте для простоты будем предполагать, что и, следовательно, . Напомним выражение для симметричной частной суммы (3.2)

,

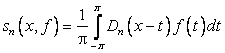Где – ядро Дирихле:

Из–за осцилляции ядра Дирихле в окрестности нуля частные суммы могут не стремиться к даже в точках непрерывности. Этого недостатка лишено ядро Фейера

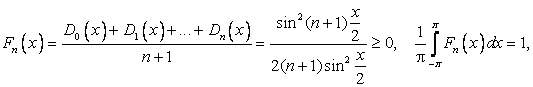
Свертка с которым представляет Среднее арифметическое Частных сумм

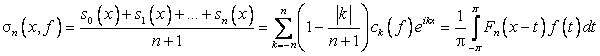Справедлива теорема 4 (Фейер) В точке скачка

, (9)

В частности, в точке непрерывности .

Аналогичным свойством обладает суммирование по Абелю–Пуассону

,

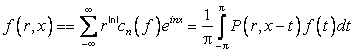Где ядро Пуассона есть

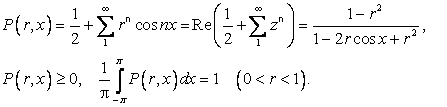
Внутри единичного круга функции и гармоничны.

Справедлива теорема 5 (Абель–Пуассон)) В точке скачка

, (10)

В частности, в точке непрерывности .

Это значит, что представляет граничные значения гармонической внутри круга функции.

Из суммируемости по Фейеру (С – суммируемость) вытекает суммируемость по Абелю–Пуассону (А – суммируемость).

< Предыдущая		Следующая >