1.5. Ряды Фурье в L2
Пространство ![]() состоит из комплекснозначных функций
состоит из комплекснозначных функций ![]() , для которых
, для которых 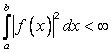 . Для таких функций определено Скалярное произведение
. Для таких функций определено Скалярное произведение
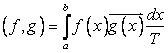 ,
,
Являющееся положительно определенной эрмитовой формой, так как
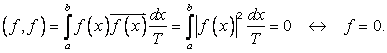
Справедлива теорема Рисса – Фишера. Пространство ![]() Полно в метрика, определяемой скалярным произведением, и, следовательно, является
Полно в метрика, определяемой скалярным произведением, и, следовательно, является
Гильбертовым пространством.
Обозначим ![]() , так как дальнейшие построения не зависят от выбора
, так как дальнейшие построения не зависят от выбора ![]() . Рассмотрим систему векторов
. Рассмотрим систему векторов ![]() . В силу соотношений (3) они попарно ортогональны и имеют длину 1. Система экспонент
. В силу соотношений (3) они попарно ортогональны и имеют длину 1. Система экспонент ![]() полна в
полна в ![]() . Этому утверждению равносильна
. Этому утверждению равносильна
Теорема 3. Тригонометрическая система полна в ![]() .
.
Лемма. Для любых положительных ![]() существует тригонометрический полином
существует тригонометрический полином ![]() со свойствами
со свойствами
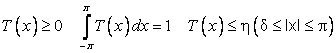
Доказательство: Рассмотрим 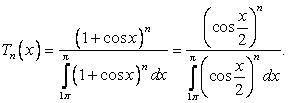
![]() очевидно, удовлетворяет первым двум условиям леммы и
очевидно, удовлетворяет первым двум условиям леммы и
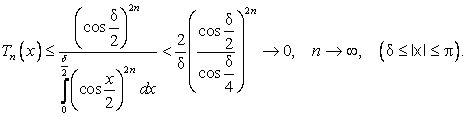
Доказательство теоремы 3: Пусть ![]() непрерывна и все ее коэффициенты Фурье равны нулю. Тогда
непрерывна и все ее коэффициенты Фурье равны нулю. Тогда
 .
.
При каждом ![]() . Пусть
. Пусть ![]() . Тогда в некоторой
. Тогда в некоторой ![]() Окрестности точки
Окрестности точки ![]()
![]() и мы получаем
и мы получаем
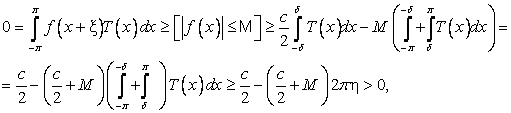
Что невозможно. Теорема 3 доказана.
Координаты вектора ![]() по ортонормированному базису
по ортонормированному базису ![]() есть коэффициенты Фурье функции
есть коэффициенты Фурье функции ![]()
 .
.
Из общих теорем об ортонормированных базисах в ![]() отсюда следует:
отсюда следует:
1. Если ![]() , то справедливо равенство Бесселя-Парсеваля
, то справедливо равенство Бесселя-Парсеваля
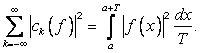
2. Ряд Фурье функции ![]() сходится к ней в среднем квадратичном.
сходится к ней в среднем квадратичном.
3. Для любой последовательности ![]() , такой что
, такой что ![]() , ряд
, ряд![]() сходится в среднем квадратичном к некоторой функции
сходится в среднем квадратичном к некоторой функции![]() ,причем
,причем![]() единственная функция, имеющая
единственная функция, имеющая ![]() своими коэффициен-тами Фурье.
своими коэффициен-тами Фурье.
Замечания.
1. В вещественном случае
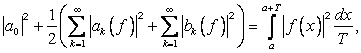
Так как ![]() .
.
2. В ![]()
![]() (Т 1), однако сходимости ряда Фурье к
(Т 1), однако сходимости ряда Фурье к ![]() нет.
нет.
3. Если ряд коэффициентов сходится абсолютно![]() , то и
, то и ![]() , поэтому
, поэтому ![]() . На самом деле ряд
. На самом деле ряд ![]() сходится равномерно к непрерывной функции.
сходится равномерно к непрерывной функции.
4. Если ![]() – произвольный тригонометрический многочлен, то квадрат его расстояния до
– произвольный тригонометрический многочлен, то квадрат его расстояния до
![]()
 очевидно,
очевидно,
минимален, если ![]()
| < Предыдущая | Следующая > |
|---|