1.3. Поточечная сходимость рядов Фурье
Пусть ![]() –
– ![]() –периодическая функция; сходится ли ( к ней ) ее разложение в ряд Фурье
–периодическая функция; сходится ли ( к ней ) ее разложение в ряд Фурье ![]() для всех точек
для всех точек ![]() на периоде? Ответ отрицательный даже для непрерывных функций. Однако справедлива, например, следующая
на периоде? Ответ отрицательный даже для непрерывных функций. Однако справедлива, например, следующая
Теорема 1. Если ![]() дважды непрерывно дифференцируема, то ее ряд Фурье сходится к ней абсолютно и равномерно.
дважды непрерывно дифференцируема, то ее ряд Фурье сходится к ней абсолютно и равномерно.
Доказательство использует важную оценку коэффициентов Фурье ![]() через ее
через ее ![]() Тую производную, обобщающую оценку (6). Для коэффициентов Фурье имеем,
Тую производную, обобщающую оценку (6). Для коэффициентов Фурье имеем, ![]() раз интегрируя по частям
раз интегрируя по частям
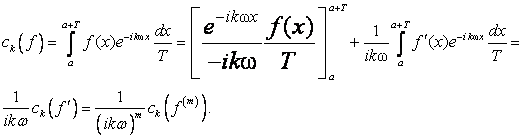
Отсюда следует оценка
 . (7)
. (7)
Которая означает, что: Чем больше у функции производных, тем быстрее стремятся к нулю ее коэффициенты Фурье.
При ![]() имеем
имеем ![]() откуда
откуда ![]() Ч. т.д.
Ч. т.д.
Важный класс функций, для которых имеет место поточечная сходимость ряда Фурье, образуют функции ограниченной вариации.
1. Вариацией ![]() Функции
Функции ![]() в промежутке
в промежутке ![]() назы
назы
вается точная верхняя грань по разбиениям ![]() про
про
межутка ![]() сумм
сумм ![]() . Функции для которых
. Функции для которых ![]() , образуют линейное пространство
, образуют линейное пространство ![]() функция ограниченной вариации (в частности, сумма и разность функция ограниченной вариации есть функция ограниченной вариации). Для Монотонной Ограниченной функции
функция ограниченной вариации (в частности, сумма и разность функция ограниченной вариации есть функция ограниченной вариации). Для Монотонной Ограниченной функции
![]() ,
,
Т. е. монотонная ограниченная функция имеет ограниченную вариацию. Обратно, каждая функция ограниченной функции есть разность двух монотонных. Ограниченные функции, встречающиеся на практике, имеют конечное число максимумов и минимумов, между которыми расположены участки монотонности; поэтому они являются функциями ограниченной вариации.
2. Если ![]() , то
, то ![]() . Действительно,
. Действительно,
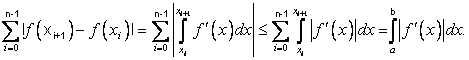
3. Функция ![]() может иметь разрывы первого рода в счетном множестве точек, однако односторонние пределы
может иметь разрывы первого рода в счетном множестве точек, однако односторонние пределы ![]() существуют во всех точках. Справедлива следующая
существуют во всех точках. Справедлива следующая
Теорема 2. (Дирихле): Пусть ![]() функция ограниченной вариации в интервале периодичности. Тогда ряд Фурье функции
функция ограниченной вариации в интервале периодичности. Тогда ряд Фурье функции ![]()
![]() условно сходится в любой точке
условно сходится в любой точке ![]() к среднему арифметическому
к среднему арифметическому ![]() пределов слева и справа. В частности, если
пределов слева и справа. В частности, если ![]() непрерывна в точке
непрерывна в точке ![]() , то ее ряд Фурье сходится условно к
, то ее ряд Фурье сходится условно к ![]() . Если
. Если ![]() непрерывна в замкнутом промежутке
непрерывна в замкнутом промежутке ![]() , то ее ряд Фурье сходится равномерно на
, то ее ряд Фурье сходится равномерно на ![]() . Условная сходимость ряда Фурье означает, что сходятся симметричные суммы
. Условная сходимость ряда Фурье означает, что сходятся симметричные суммы ![]() ; при этом например, суммы
; при этом например, суммы ![]() ,
, ![]() могут расходится. В то же время ряды по косинусам и синусам в отдельности сходятся, так как являются рядами Фурье функций
могут расходится. В то же время ряды по косинусам и синусам в отдельности сходятся, так как являются рядами Фурье функций ![]() .
.
Доказательство теоремы 2 основано на вытекающем из соотношений ортогональности (1.3) представлении симметричной частной суммы как свертки с Ядром Дирихле ![]()
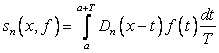 , (8)
, (8)
Где 
| < Предыдущая | Следующая > |
|---|