1.2. Примеры разложений в ряд Фурье

1. Разложить в ряд Фурье в промежутке . Отметим,

что имеет один разрыв на периоде в точке . Имеем ,

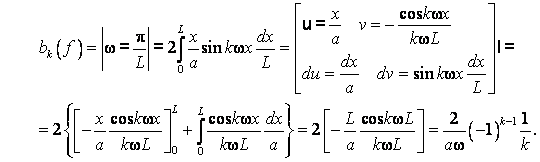
В частности, при и мы получаем разложение

,

Из которого заменой следует известная формула

Можно доказать, что

2. Разложить непрерывную в промежутке функцию

В ряд Фурье по синусам. Имеем .

.

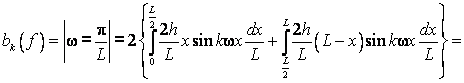
Отсюда

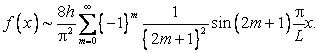
Так как числовой ряд обратных квадратов сходится, ряд Фурье сходится абсолютно и мы имеем

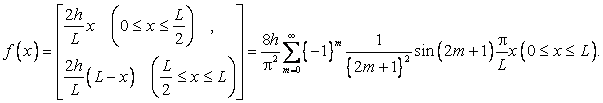
3. Разложить ту же функцию в ряд Фурье по косинусам в промежутке . Имеем

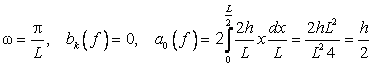
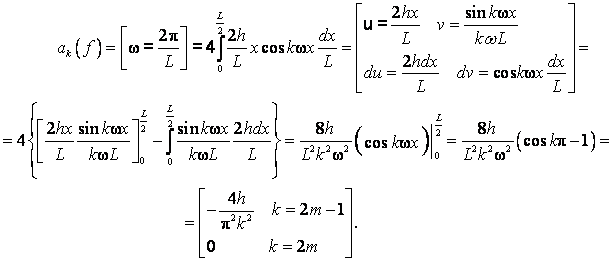
Отсюда

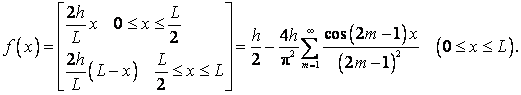
При Получаем, в частности

.

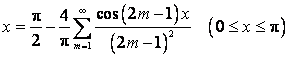4. Разложить в ряд Фурье по косинусам в промежутке . Имеем ,,

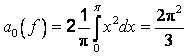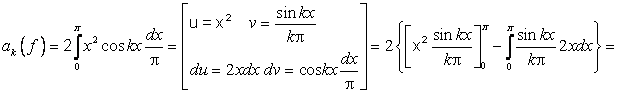
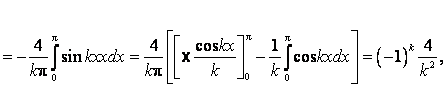
Так что .

При Получаем, в частности,

,

А при

.

5. Разложить в ряд Фурье в промежутке .. Здесь Обращается в бесконечность На концах промежутка, оставаясь при этом несобственно интегрируемой, . Ввиду четности функции . Имеем для , используя известный интеграл Эйлера

:

.

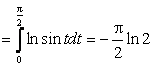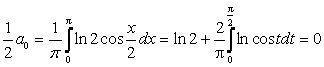Аналогично для , используя выражение для ядра Дирихле (см. 1.3.)

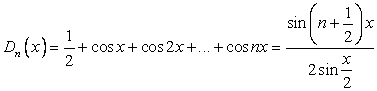
Имеем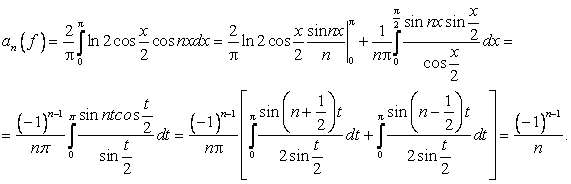

Таким образом, окончательно получаем 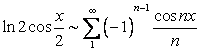. Это разложение сходится при , что дает равенство

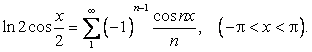
Заменяя на , получаем

.

Формально дифференцируя последний ряд, получаем разложение Фурье (неинтегрируемой!) функции :

.

Это разложение справедливо в смысле теории обобщенных функций (распределений) (см. 2.7.)

В заключение приведем примеры выполнения расчетно-графических заданий.

1. Разложить периодическую с периодом функцию в ряд Фурье.

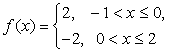
Имеем .

;

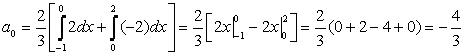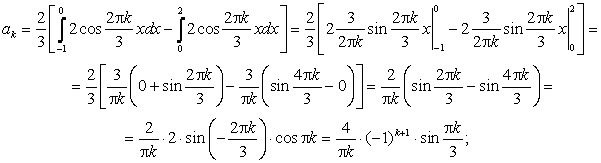
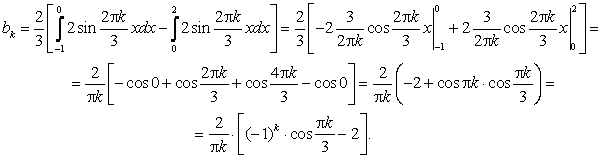Окончательно,

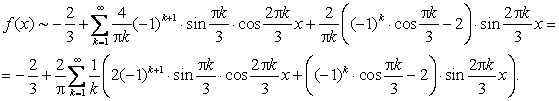
2. Разложить функцию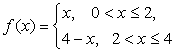

В ряд Фурье по синусам. Имеем

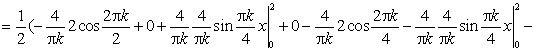
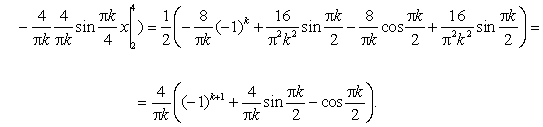
Окончательно,

.

< Предыдущая		Следующая >