1.1. Ряды Фурье. Гармонический анализ периодических функций
Комплекснозначная функция 
числового аргумента 
имеет Период 
, если 
. Если 
– период, то его целые кратные – тоже периоды. Наименьший из периодов непостоянной функции 
называется Основным, остальные кратны ему
Из формулы Эйлера 
следует, что Экспонента 
имеет период , если 
, или 
. Число 
называется Частотой, Соответствующей периоду . При 
, при 
получается функция, по модулю равная единице, с основным периодом 
. Это Гармоники С периодом .
Пусть –периодическая функция, допускающая период . Основная задача гармонического анализа состоит в разложении в ряд по гармоникам, имеющим период
(1)
При суммировании ряда (1) обычно группируют слагаемые с противоположными индексами
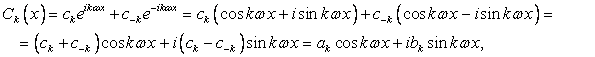Где 
Если 
, 
вещественны и ряд (1) представляет вещественную функцию. В этом случае имеем разложение в Тригонометрической форме
(2)
Если ряд (1) можно интегрировать почленно (что обеспечено, напри-
Мер, в простом случае 
), то коэффициенты 
определяются функцией Однозначно. Действительно, положив 
и интегрируя почленно, имеем
,
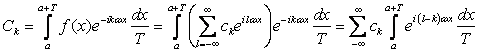Откуда, учитывая Соотношения ортогональности
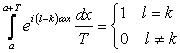, (3)
Получим 
.
Кроме того, для любой 
Периодической функции интеграл в 
не зависит от 
; действительно
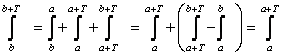
Числа
(4)
Определены для любой суммируемой функции (т. е.
) и называются Коэффициентами Фурье Функции . Для коэффициентов тригонометрического разложения (2) имеем
(5)
Из (4), (5) вытекают такие следствия:
1. Если функция четна, то
.
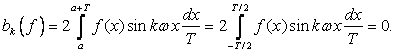При этом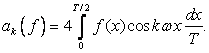 
.
2. Если функция нечетна, то
.
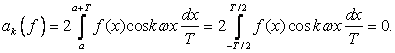При этом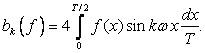 
.
3. Если функция имеет период 
(
Натуральное), то отличны от нуля только коэффициенты Фурье с номерами, кратными 
, так как можно разложить по гармоникам 
, имеющим период .
4. Если – Произвольная Функция на промежутке 
, то ее разложением в ряд Фурье называется разложение в ряд Фурье ее периоди-
Ческого продолжения, при этом 
.
5. Разложением в ряд Фурье по косинусам в промежутке 
называется разложение в ряд Фурье четной, 
Периодической функции, совпадающей с в промежутке .
6. Разложением в ряд Фурье по синусам в промежутке называется разложение в ряд Фурье нечетной, Периодической функции, совпадающей с в промежутке .
Оценки коэффициентов Фурье
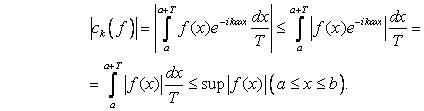(6).
Отсюда
.
Справедлива более сильная
Теорема 1 (Лебег): Для суммируемой функции 
.
| Следующая > |
|---|
