6.1. Вычисление предела дробно-рациональной функции
6.1.1. Вычисление предела дробно - рациональной функции при ![]()
Пусть ![]() и
и ![]() – многочлены соответственно степеней
– многочлены соответственно степеней ![]() и
и ![]() .
.
Выражение 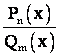 при
при ![]() может не представлять собой неопределённости или быть отношением двух бесконечно малых. При вычислении
может не представлять собой неопределённости или быть отношением двух бесконечно малых. При вычислении  могут представляться следующие случаи.
могут представляться следующие случаи.
А. Выражение 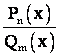 не представляет собой неопределённости, если
не представляет собой неопределённости, если ![]() - не является корнем знаменателя, то есть
- не является корнем знаменателя, то есть ![]() . В этом случае используют теорему об арифметических действиях над функциями, имеющими предел в точке:
. В этом случае используют теорему об арифметических действиях над функциями, имеющими предел в точке:

Б. Не представляет никакого труда вычисление предела и в случае, если ![]() – корень знаменателя, но не является корнем числителя, то есть
– корень знаменателя, но не является корнем числителя, то есть ![]() ,
, ![]() . В этом случае отношение
. В этом случае отношение 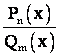 При
При ![]() является бесконечно большой функцией, поэтому
является бесконечно большой функцией, поэтому  .
.
В. Если же ![]() является и корнем числителя и корнем знаменателя:
является и корнем числителя и корнем знаменателя: ![]() ,
, ![]() , то выражение
, то выражение 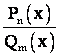 При
При ![]() представляет собой неопределённость типа
представляет собой неопределённость типа ![]() . В этом случае в числителе и в знаменателе можно выделить общий множитель наибольшей степени
. В этом случае в числителе и в знаменателе можно выделить общий множитель наибольшей степени ![]() и сократить на него. Выделить такой множитель можно либо с помощью деления многочленов на
и сократить на него. Выделить такой множитель можно либо с помощью деления многочленов на ![]() «в столбик», либо путём группировки слагаемых. После сокращения на
«в столбик», либо путём группировки слагаемых. После сокращения на ![]() приходим либо к случаю А, либо к случаю Б.
приходим либо к случаю А, либо к случаю Б.
Пример 1. Вычислить ![]() .
.
Решение. Число ![]() не является корнем знаменателя:
не является корнем знаменателя: ![]() (случай А), поэтому
(случай А), поэтому
 .
.
Пример 2. Вычислить 
Решение. Здесь ситуация такая же: число 2 не является корнем знаменателя (хотя и является корнем числителя).
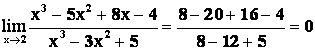
Пример 3. Вычислить 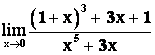
Решение. В данном случае число ![]() является корнем знаменателя, но не является корнем числителя (случай Б)
является корнем знаменателя, но не является корнем числителя (случай Б)

Пример 4. Вычислить ![]()
Решение. В этом случае ![]() является корнем и числителя, и знаменателя, а значит выражение представляет собой неопределённость
является корнем и числителя, и знаменателя, а значит выражение представляет собой неопределённость ![]() . В знаменателе следует выделить множетель
. В знаменателе следует выделить множетель ![]() . Возможно этот множитель будет входить в некоторой степени (если корни кратные). В числителе выделить такой множитель несложно:
. Возможно этот множитель будет входить в некоторой степени (если корни кратные). В числителе выделить такой множитель несложно:
![]()
Для того чтобы выделить такой множитель в знаменателе удобно разделить знаменатель на ![]() “в столбик”. Такое деление возможно без остатка по следствию из теоремы Безу. Действительно:
“в столбик”. Такое деление возможно без остатка по следствию из теоремы Безу. Действительно:

Теперь знаменатель можно представить как произведение:
![]()
Окончательно: 
6.1.2 Вычисление предела дробно – рациональной функции при ![]()
Пусть при ![]() дробно-рациональная функция представляет собой неопределённость типа
дробно-рациональная функция представляет собой неопределённость типа ![]() . Тогда при вычислении
. Тогда при вычислении  полезно учитывать, что при
полезно учитывать, что при ![]()
![]()
![]()
Поэтому

Пример 6.
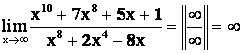
![]() ;
;
Пример 7.

![]() ;
;
Пример 8.
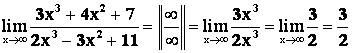 .
.
Если многочлены в числителе и знаменателе не представлены в стандартном виде, нужно внимательно отнестись к определению старшей степени. Например, выражение ![]() является многочленом третьей, а не четвёртой степени.
является многочленом третьей, а не четвёртой степени.
| < Предыдущая | Следующая > |
|---|