6.2. Вычисление пределов функций, содержащих
При вычисление пределов вида 
в случае если числи-
Тель или знаменатель содержит выражение 
, стремящееся к нулю при 
часто бывает полезным избавиться от иррациональности в числителе или в знаменателе путём домножения числителя и знаменателя на соответствующий сопряжённый множитель 
.
Для разности 
таким множителем является 
, для выражения 
таким множителем является 
.
В самом деле
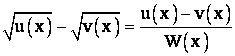, где ,
,
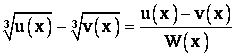Где 
.
В общем случае для разности 
сопряжённое выражение 
. В результате умножения получаем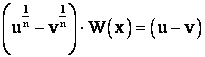 
, т. е. 
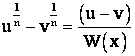. Для сокращения записи 
можно вычислить отдельно и если он конечен и не равен нулю, вынести за знак предела.
Пример 1
A =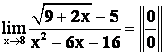 
Решение: Т. к. х
8, то х-80. Выделим множитель 
в числителе и знаменателе. Умножим числитель и знаменатель дроби на множитель 
. Тогда в числителе мы получим
В знаменателе множитель будет стремиться к конечному пределу, не равному 0, а именно к 10 при х8, поэтому по теореме о пределе
Произведения множитель 
можно вынести за знак предела. Знаменатель представим в виде произведения х2 – 6х – 16 = (х – 8)(х + 2). Таким образом, вычисление данного предела сводиться к следующим действиям:
A =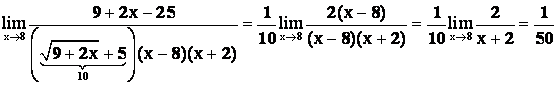 
Пример 2. Вычислить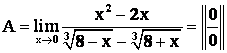 
Решение: Выделим в числителе и знаменателе множитель, стремящийся к нулю, т. е. х.
Числитель: 
Знаменатель:
.
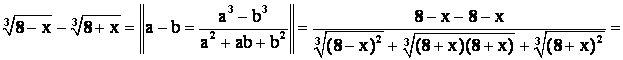
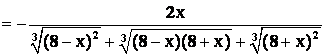Таким образом, предел приобретает вид
A =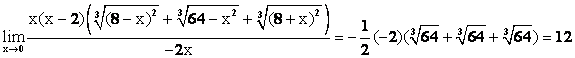 
Пример 3.
A =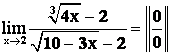 
Решение: Выделим в числителе и знаменателе множитель, стремящийся к 0, т. е. (х – 2)
Числитель:
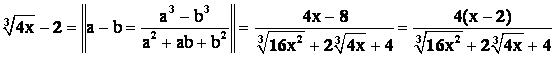
Знаменатель: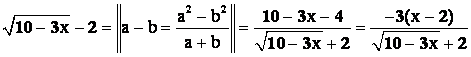 
.
Тогда A =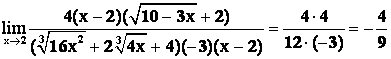 
.
Пример 3.
A =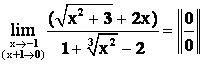 
Решение: Как и в предыдущем случае выделим множитель, стремящийся к 0, т. е. (х+1) в числителе и знаменателе. Тогда
Числитель: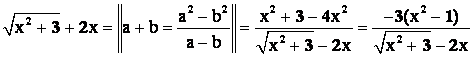 
.
Знаменатель: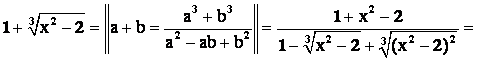 
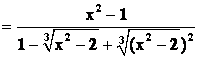
Таким образом
A =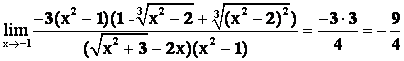 
При раскрытии неопределенностей вида 
нужно выполнить тождественные преобразования, позволяющие свести такую неопределенность к виду 
или 
. Например, в случае, если выражение содержит иррациональности с невысоким показателем корня, этого можно добиться путем умножения и деления данного выражения на «сопряженное».
Пример 5.
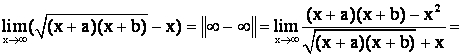
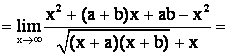
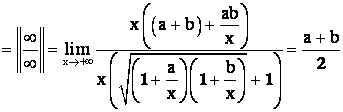
Пример 6.
(Сумма двух бесконечно больших одного знака есть величина бесконечно большая)
Пример 7.
Решение. Данный предел содержит корень с высоким показателем, поэтому умножение и деление на сопряженное выражение нецелесообразно. Преобразуем данное выражение следующим образом:
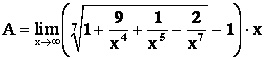
При 
выражение 
, т. е. является бесконечно малой величиной. Если воспользоваться следствием из 2-го замечательного предела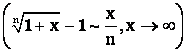 
, то выражение, стоящее в скобках, можно заменить эквивалентной величиной 
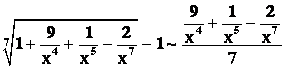. Так как величина 
является бесконечно малой более высокого порядка, чем 
, то ее можно отбросить, поэтому данная дробь будет эквивалентна выражению 
.
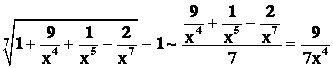Следовательно,
Пример 8.
Решение. Выделим Главную часть в каждом из слагаемых. Очевидно, что при
;
.
Таким образом, оба радикала имеют одинаковую часть 
. Вычтем ее из каждого радикала. Тогда получим
=
.
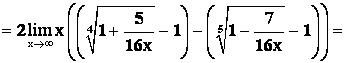
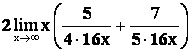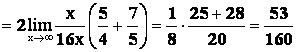Пример 9.
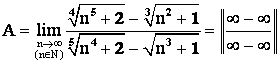
Решение. 1 Способ: Выделим главную часть числителя и знаменателя. Т. к. 
то главная часть числителя будет совпадать с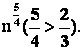 
Аналогично, 
поэтому главная часть знаменателя совпадает с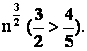 
Тогда 
2 способ: Вынесем из-под каждого корня старшую степень переменной.
При раскрытии неопределенностей вида 
можно также выделить главную часть числителя и знаменателя.
Пример 10.
Решение. 1 способ:Этот пример можно решить, воспользовавшись для выделения главной части эквивалентными бесконечно большими величинами, а именно:
Значит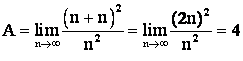 
2 способ: Этот же предел можно вычислить и непосредственно, а именно вынести за скобки старшую степень переменной в числителе и знаменателе.
Пример 11.
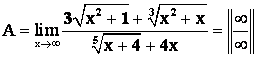
Решение: 1 способ: Как и в предыдущем примере, выделим главную часть числителя и знаменателя.
, 
Тогда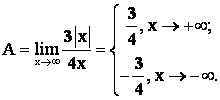 
2 способ: Вынесем в числителе и знаменателе за скобки старшую степень х.
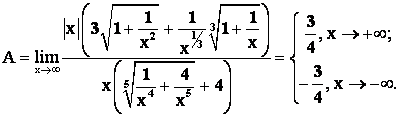
| < Предыдущая | Следующая > |
|---|
