4.4. Сравнение бесконечно больших функций

Пусть функции и положительные бесконечно большие при .

Говорят, что функция при имеет более высокий порядок

Роста, чем функция , если

.

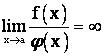Если предел конечен и не равен нулю или единице, то функции и называются бесконечно большими одного порядка роста при .

Если же

,

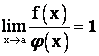То функции и называются эквивалентными.

< Предыдущая		Следующая >