4.3 Сравнение бесконечно малых функций

Существенно облегчает раскрытие неопределенностей использование сравнения бесконечно малых и бесконечно больших функций.

Пусть функции , и – бесконечно малые функции при .

Def 5 Бесконечно малую при функцию называют бесконечно малой более высокого порядка малости, чем функция , если .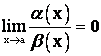

Обозначение: .

Def 6 Бесконечно малые функции и являются бесконечно малыми одного порядка, если существует конечный 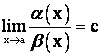. Обозначение: .

Def 7 Если предел отношения функций и при равен 1, то и называются эквивалентными при . Обозначение: , .

Основные соотношения эквивалентности следуют из первого и второго замечательных пределов.

Приведём Таблицу эквивалентных При

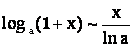
Заметьте, что если при , то всюду в этой таблице можно писать вместо , например , .

Вычисление пределов существенно облегчают следующие Свойства эквивалентных бесконечно малых:

1. Если , а при , то 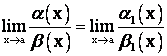. Это позволяет при вычислении пределов в отношениях заменять бесконечно малые более простыми эквивалентными выражениями.

2. Отношение эквивалентности транзитивно: если , а .

3. Если , то . Это обстоятельство часто позволяет при вычислении пределов отбрасывать бесконечно малые более высоких порядков.

4. Для того чтобы две бесконечно малые при функции и были эквивалентны необходимо и достаточно, чтобы их разность была бесконечно малой более высоко порядка малости, чем каждая из них.

Из этого следует, что при вычислении пределов в разности двух бесконечно малых делать замены эквивалентными нельзя. Убедитесь на примерах:

Пусть , и .

Поскольку при , то разность .

При вычислении предела может быть важно, какого именно порядка малости эта разность. Вычисления показывают, что эта разность эквивалентна :

,

Если же заменить каждую из этих величин эквивалентной, например таким образом , , , то придем к заведомо неправильному результату , .

< Предыдущая		Следующая >