4.2 Бесконечно большие и бесконечно малые функции
Def 4 (по Коши). Говорят, что предел функции ![]() при
при ![]() равен
равен ![]() , и пишут
, и пишут ![]() , если
, если ![]() найдется такая
найдется такая ![]() – окрестность точки
– окрестность точки ![]()
![]() , что для всех
, что для всех ![]()
![]() .
.
Если ![]() – конечная точка, то это определение можно записать так:
– конечная точка, то это определение можно записать так: ![]()
![]()
![]() .
.
Функция ![]() , имеющая бесконечный предел при
, имеющая бесконечный предел при ![]() называется бесконечно большой при
называется бесконечно большой при ![]() .
.
Функция ![]() называется бесконечно малой при
называется бесконечно малой при ![]() , если
, если ![]() .
.
Перечислим основные свойства бесконечно малых и бесконечно больших функций, наиболее важные при практическом вычислении пределов.
1. Сумма (разность) конечного числа бесконечно малых функций при ![]() есть бесконечно малая функция при
есть бесконечно малая функция при ![]() .
.
2. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
3. Произведение бесконечно больших функций при ![]() есть бесконечно большая при
есть бесконечно большая при ![]() .
.
4. Если ![]() при
при ![]() - бесконечно большая, то
- бесконечно большая, то 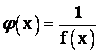 – бесконечно малая и наоборот: если
– бесконечно малая и наоборот: если ![]() при
при ![]() бесконечно малая и существует окрестность точки
бесконечно малая и существует окрестность точки ![]() , в которой
, в которой ![]() , то
, то 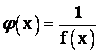 – бесконечно большая при
– бесконечно большая при ![]() .
.
5. Если функции ![]() и
и ![]() при
при ![]() – бесконечно большие одного знака, то их сумма также является бесконечно большой при
– бесконечно большие одного знака, то их сумма также является бесконечно большой при ![]() .
.
Если к выражению, предел которого нужно вычислить, возможно применить теорему об арифметических действиях или перечисленные свойства, то вычисление предела трудности не представляет.
В большинстве же случаев непосредственное применение этих теорем невозможно. Такие случаи, в частности, имеют место, если выражение, предел которого нужно найти, представляется в виде:
А. Отношения двух функций, каждая из которых бесконечно малая (в этом случае говорят, что имеет место неопределенность ![]() ) или
) или ![]()
Б. Отношения двух функций, каждая из которых бесконечно большая (неопределённость ![]() )
)
В. Произведение двух функций, одна из которых бесконечно малая, а другая бесконечно большая (неопределённость ![]() )
)
Г. Разности двух функций, имеющих бесконечные пределы одного знака (неопределённость ![]() ).
).
При вычислении пределов степенно-показательных выражений возникают неопределённости типа ![]() ,
, ![]() ,
, ![]() .
.
Во всех этих случаях необходимо преобразовать выражение так, чтобы избавиться от неопределенности или свести вопрос к известному пределу. Среди известных пределов наиболее важны два замечательных предела и следствия из них:
I замечательный предел:
![]() .
.
Следствия из I-го замечательного предела:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
II замечательный предел:
 Е
Е
Или ![]() Е,
Е,
Где е![]()
Следствия из II - го замечательного предела:
![]() ,
,
 ,
,
![]() ,
,
 .
.
![]()
| < Предыдущая | Следующая > |
|---|