4.1 Различные определения предела функции в точке

(предельного значения функции)

Пусть функция определена на множестве Х, точка А – предельная точка этого множества.

Понятие предела функции в точке (предельного значения функции) можно определить через последовательности (по Гейне) и с использованием понятия окрестности точки (по Коши).

Def 1 (по Гейне). Число А называется пределом функции при А (или её предельным значением), если для любой последовательности , сходящейся к числу А соответствующая последовательность значений функции стремится к числу А

Обозначение:

Def 2 (по Коши). Число А называется пределом функции при , если любой – окрестности точки соответствует такая проколотая – окрестность точки что для всех точек этой окрестности значение функции принадлежит – окрестности точки А, т. е.

Или другими словами

Определения по Коши и по Гейне эквивалентны.

Если является точкой сгущения множества Х, то можно определить предел функции при .

По Коши предел функции при определяется так:

Def 3 Число называется пределом функции при , если

R

Обозначение: .

Аналогично определяется по Коши предел функции при .

Поскольку понятие предела функции может быть определено через последовательности (по Гейне), то и свойства функции, имеющей предел в точке, совпадают со свойствами сходящихся последовательностей, в частности арифметические действия над функциями, имеющими предел при (А может быть и ), приводят к функциям, также имеющим предел при .

Имеет место

Теорема 1. Пусть – множество определения функций и , – предельная точка множества и при существуют пределы этих функций:

,

Тогда

1. R

2.

3.

4. Если , то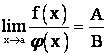

< Предыдущая		Следующая >