3.2. Примеры решения задач
Задание 1. Доказать, используя определение предела последовательности, что 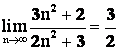 . Найти номер элемента последовательности, начиная с которого последовательность отличается от своего предела не более, чем на 0,001.
. Найти номер элемента последовательности, начиная с которого последовательность отличается от своего предела не более, чем на 0,001.
Решение. Доказать, что ![]() – это значит
– это значит ![]() указать такой номер
указать такой номер ![]() , что все элементы последовательности, начиная с этого номера, не больше чем на
, что все элементы последовательности, начиная с этого номера, не больше чем на ![]() по модулю отличаются от
по модулю отличаются от ![]() .
.
В нашем случае
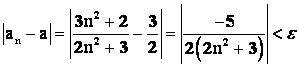 ;
;
 .
.
Если ![]() достаточно большое настолько, что
достаточно большое настолько, что ![]() , то равенство выполняется
, то равенство выполняется ![]() . Значит, для
. Значит, для ![]() в качестве
в качестве ![]() можно выбрать 1.
можно выбрать 1.
Если ![]() , то из неравенства
, то из неравенства ![]() следует, что
следует, что 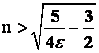 и в качестве
и в качестве ![]() можно выбрать любое натуральное число, удовлетворяющее неравенству, например
можно выбрать любое натуральное число, удовлетворяющее неравенству, например 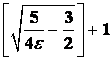 (
(![]() – целая часть числа
– целая часть числа ![]() ).
).
Итак, 
При ![]()
![]() .
.
Задание 4. Доказать, что последовательность 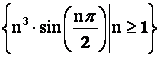 является неограниченной, но не является бесконечно большой.
является неограниченной, но не является бесконечно большой.
Решение. Решение состоит из двух частей. Доказать, что последовательность неограниченна, т. е. ![]() , другими словами, последовательность содержит сколь угодно большие элементы. Тем не менее, эта последовательность не является бесконечно большой, т. е. для последовательности неверно утверждение
, другими словами, последовательность содержит сколь угодно большие элементы. Тем не менее, эта последовательность не является бесконечно большой, т. е. для последовательности неверно утверждение ![]() , а верно обратное утверждение
, а верно обратное утверждение ![]() . Другими словами, в последовательности есть элементы со сколь угодно большими номерами, модуль которых не превосходит некоторого числа.
. Другими словами, в последовательности есть элементы со сколь угодно большими номерами, модуль которых не превосходит некоторого числа.
В данном случае 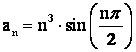 . При
. При ![]() – нечётных
– нечётных ![]()
![]() , при
, при ![]() - чётных
- чётных ![]()
![]() .
.
Докажем первую часть утверждения. Выберем произвольное сколь угодно большое ![]() и найдём такой номер
и найдём такой номер ![]() , что
, что ![]() . Если
. Если ![]() нечётно, то
нечётно, то ![]() . Из неравенства
. Из неравенства ![]() следует, что в качестве
следует, что в качестве ![]() можно выбрать любое нечётное число, большее, чем
можно выбрать любое нечётное число, большее, чем ![]() .
.
Чтобы доказать вторую часть утверждения, обратим внимание на то, что все элементы последовательности с чётными номерами ![]() . Если
. Если ![]() (например
(например ![]() ), то какой бы мы ни указали номер
), то какой бы мы ни указали номер ![]() , найдется номер
, найдется номер ![]() больше
больше ![]() (чётный), такой, что
(чётный), такой, что ![]() .
.
Таким образом, последовательность не является бесконечно большой.
Задание 5.
Пример 1. Доказать, что последовательность ![]() имеет предел.
имеет предел.
![]()
![]()
![]()
Решение. Покажем, что последовательность ![]() монотонно возрастающая.
монотонно возрастающая.
![]()
![]()
Сравним последовательность ![]() с последовательностью
с последовательностью ![]()
![]() , каждый член
, каждый член ![]() – сумма
– сумма ![]() членов геометрической прогрессии со знаменателем
членов геометрической прогрессии со знаменателем 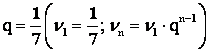 .
.
Сумма ![]() членов геометрической прогрессии определяется по формуле
членов геометрической прогрессии определяется по формуле  , т. е.
, т. е.  , при
, при ![]() имеем
имеем 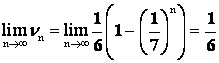 .
.
Так как ![]() , то
, то ![]() . Итак, все условия теоремы о сходимости монотонной и ограниченной последовательности выполнены, следовательно, последовательность
. Итак, все условия теоремы о сходимости монотонной и ограниченной последовательности выполнены, следовательно, последовательность ![]() имеет предел. Обратите внимание на то, что
имеет предел. Обратите внимание на то, что ![]() не является
не является ![]() , поэтому нельзя утверждать, что
, поэтому нельзя утверждать, что ![]() .
.
Пример 2. Доказать, что последовательность ![]()
![]() имеет предел, и вычислить его.
имеет предел, и вычислить его.
Решение. Покажем, что последовательность:
А) ограничена сверху;
Б) монотонно возрастает.
При доказательстве пункта а) используем метод математической индукции. Очевидно, что ![]() . Предположим, что для произвольного номера
. Предположим, что для произвольного номера ![]() выполняется неравенство
выполняется неравенство ![]() , тогда
, тогда ![]() . В соответствии с методом математической индукции неравенство выполняется для любого номера, т. е.
. В соответствии с методом математической индукции неравенство выполняется для любого номера, т. е. ![]() , следовательно, последовательность ограничена сверху. б) Докажем, что
, следовательно, последовательность ограничена сверху. б) Докажем, что ![]() , снова используя метод математической индукции. Очевидно, что
, снова используя метод математической индукции. Очевидно, что ![]() . Пусть
. Пусть ![]() .
.
![]() .
.
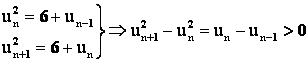
![]() , но так как
, но так как ![]() , то
, то ![]() , значит,
, значит, ![]() для
для ![]() .
.
Таким образом, последовательность ![]() монотонно возрастает и ограничена сверху, значит, она имеет предел. Вычислим его. Пусть
монотонно возрастает и ограничена сверху, значит, она имеет предел. Вычислим его. Пусть ![]() . Так как
. Так как ![]() , то
, то ![]() . Поскольку
. Поскольку
![]() , но
, но ![]() ,
, ![]() , тогда
, тогда ![]() ,
, ![]() . Так как мы установили, что
. Так как мы установили, что ![]() , то
, то ![]() отбрасываем. Итак
отбрасываем. Итак ![]() .
.
При выполнении заданий 6, 7, 8 используется следующий результат

Задание 6. Вычислить предел 
Решение. При нахождении предела отношения двух многочленов необходимо сравнить степени ![]() в числителе и в знаменателе. При кажущейся простоте этой операции она требует определенного внимания и навыков. Рассмотрим предел
в числителе и в знаменателе. При кажущейся простоте этой операции она требует определенного внимания и навыков. Рассмотрим предел  =
=![]() Приведем подобные члены
Приведем подобные члены![]()

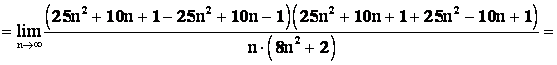

Так как наивысшие степени ![]() в числителе и знаменателе равны между собой
в числителе и знаменателе равны между собой ![]() , то предел равен отношению коэффициентов при наивысших степенях.
, то предел равен отношению коэффициентов при наивысших степенях.
Задание 7. Вычислить предел 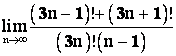 .
.
Решение. Отметим, что
![]() ;
; ![]() ,
,
Тогда 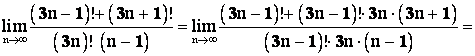
 .
.
В следующем задании предлагается найти предел выражения, которое представляет собой сумму, число слагаемых которой возрастает с ростом ![]() . В этом случае нельзя переходить к пределу в каждом слагаемом отдельно. Предел можно вычислить, предварительно просуммировав слагаемые под знаком предела. С этой целью используются известные формулы суммирования
. В этом случае нельзя переходить к пределу в каждом слагаемом отдельно. Предел можно вычислить, предварительно просуммировав слагаемые под знаком предела. С этой целью используются известные формулы суммирования ![]() членов арифметической и геометрических прогрессий.
членов арифметической и геометрических прогрессий.
Задание 8.
Пример 1. Найти предел числовой последовательности
 .
.
Решение. Преобразуем заданное выражение
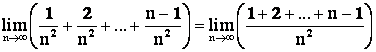 .
.
В числителе стоит сумма ![]() членов арифметической прогрессии со знаменателем
членов арифметической прогрессии со знаменателем ![]() . Сумма
. Сумма ![]() членов арифметической прогрессии равна
членов арифметической прогрессии равна ![]() . В нашем примере
. В нашем примере ![]() ,
, ![]() , число членов
, число членов ![]() , тогда
, тогда ![]() .
.
![]()
 .
.
Пример 2. Найти предел числовой последовательности
 .
.
Решение. Преобразуем заданное выражение
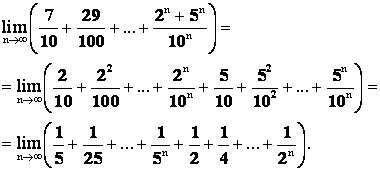
Таким образом, мы имеем сумму ![]() членов двух геометрических прогрессий, знаменатель одной из них
членов двух геометрических прогрессий, знаменатель одной из них ![]() , первый член
, первый член ![]() , знаменатель другой
, знаменатель другой ![]() , первый член
, первый член ![]() .
.
Сумма ![]() членов геометрической прогрессии определяется по формуле
членов геометрической прогрессии определяется по формуле  , т. е.
, т. е.
Для первой прогрессии 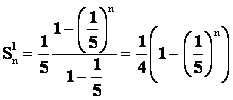 ,
,
Для второй прогрессии  ,
,
При ![]() имеем
имеем

Задание 9.
Пример 1. Вычислить предел
![]() .
.
Решение.
![]()
Для раскрытия неопределённости воспользуемся соотношением
![]()
И домножим числитель и знаменатель на сопряжённое выражение

При вычислении предела было учтено, что ![]() ,
, ![]() .
.
Пример 2. Вычислить предел
![]() .
.
Решение.
![]()
Для раскрытия неопределённости воспользуемся соотношением ![]() и домножим числитель и знаменатель на сопряжённое выражение
и домножим числитель и знаменатель на сопряжённое выражение

Задание 10. Вычислить предел  .
.
Решение. Так как 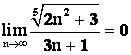 , то
, то 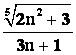 – величина бесконечно малая,
– величина бесконечно малая, ![]() , т. е.
, т. е. ![]() – величина ограниченная. Произведение величины ограниченной на бесконечно малую есть величина бесконечно малая, т. е.
– величина ограниченная. Произведение величины ограниченной на бесконечно малую есть величина бесконечно малая, т. е.
 .
.
| < Предыдущая | Следующая > |
|---|