3.1 Примеры выполнения теоретических упражнений

Упражнение 1. Последовательность сходится, последовательность расходится. Может ли сходится последовательность ?

Допустим, что последовательность = сходится. Тогда является разностью двух сходящихся последовательностей, а значит, сама сходится, что противоречит условию.

Ответ: сумма двух последовательностей, одна из которых сходится, а другая расходится, всегда расходится.

Упражнение 2. Две последовательности расходятся, может ли сходиться их сумма?

Сумма двух расходящихся последовательностей может сходиться, но может и расходиться. Это можно показать, приведя два примера.

Пример 1. Последовательность –1, 1, –1, 1, –1,… – расходится, последовательность 1, –1, 1, –1, 1,… – расходится, их сумма = 0, 0, 0, 0, 0,… – сходится.

Пример 2. Последовательности и расходятся, их сумма – расходится.

Упражнение 3. Приведите пример такой последовательности , которая ограничена, , а не существует.

Очевидно, что такой пример следует искать среди последовательностей, которые не являются монотонными, поскольку монотонные и ограниченные последовательности предел имеют.

Последовательность удовлетворяет всем условиям упражнения:

А) очевидно, что предела не имеет;

Б) она ограничена ,

В).

Под знаком предела произведение ограниченной величины на величину бесконечно малую:

;

.

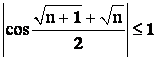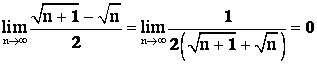< Предыдущая		Следующая >