1.5. Признаки существования предела числовой последовательности

Def 7. Число а называется пределом числовой последовательности , если

.

Используя понятие окрестности точки, это определение можно сформулировать так:

Def 8. Число называется пределом числовой последовательности , если для любой – окрестности точки а существует такой номер N (определяемый – окрестностью), что все элементы последовательности, номера которых больше N, содержатся в указанной окрестности.

Данные определения означают, что какую бы точность мы ни задали, найдется номер N, такой, что абсолютная погрешность приближения числа а элементами последовательности меньше , как только номер приближения n больше N.

Символически тот факт, что последовательность своим пределом имеет число записывается так:

.

Пределом бесконечно большой последовательности считают и обозначают .

Последовательность, имеющая конечный предел, называется сходящейся; последовательности, не имеющие предела и бесконечно большие последовательности – расходящимися.

Среди признаков существования предела последовательности (признаков сходимости) отметим три наиболее важных. Критерий Коши и два достаточных признака:

Теорема 1 (критерий Коши). Для того чтобы последовательность сходилась необходимо и достаточно, чтобы N .

А также два достаточных признака:

Теорема 2. Если последовательность монотонно возрастает и ограничена сверху, то она сходится. (Аналогичный признак для монотонно убывающей и ограниченной снизу последовательности)

Теорема 3. Пусть и – две последовательности, сходящиеся к одному и тому же пределу а. Если последовательность удовлетворяет неравенству N, то она тоже сходится к пределу а.

Свойства сходящихся последовательностей

1. Последовательность не может сходиться к двум различным пределам.

2. Сходящаяся последовательность ограничена.

3. Арифметические действия над сходящимися последовательностями приводят к сходящимся последовательностям:

Если и сходятся и пределы их соответственно равны a и b, то:

а) сходится и

б) сходится и

в) сходится и

г) Если , то сходится и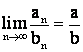

4. Если начиная с некоторого номера N элементы двух сходящихся последовательностей и связаны неравенством , то их пределы связаны тем же неравенством .

< Предыдущая		Следующая >