1.4. Арифметические действия над последовательностями

Пусть и – две числовые последовательности. Последовательность называется суммой и , - их произведением. Если среди элементов последовательности нет равных нулю, то можно определить частное двух последовательностей .

Пусть, например, 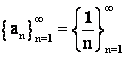; , т. е.

.

.

Тогда

.

.

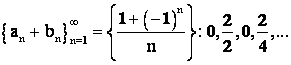
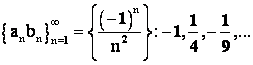При работе с бесконечно большими последовательностями нужно помнить, что:

· сумма двух бесконечно больших последовательностей одного знака является бесконечно большой;

· произведение двух бесконечно больших последовательностей является бесконечно большой.

· отношение двух бесконечно больших и разность двух бесконечно больших последовательностей одного знака представляют собой не-

Определенности типов и .

< Предыдущая		Следующая >