1.2. Бесконечно большие последовательности

Def 2. Последовательность называется ограниченной сверху, если сверху ограниченно множество её значений, т. е. N , ограниченной снизу, если N и ограниченной, если она ограничена сверху и снизу.

Def 3. Последовательность называется неограниченной сверху, если она содержит элементы, большие любого наперед данного числа, т. е. N . Аналогично определяется неограниченность снизу.

Последовательность 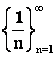ограничена сверху и снизу, т. к. N

.

Легко доказать, что при геометрическая прогрессия ограниченна, при ограниченной не является.

Докажем, что не является ограниченной, например, последовательность .

В самом деле, сколь большим бы ни было число M, найдется элемент последовательности , больший M: . Для этого должно выполняться условие . Этому условию удовлетворяет, например, первое целое число, большее, чем : .

Def 4. Последовательность называется бесконечно большой, если начиная с некоторого номера её элементы по абсолютной величине больше любого наперед заданного числа, т. е.

.

Бесконечно большой является, например, . В самом деле: выберем любое положительное число M. Тогда неравенство будет выполняться для всех , т. е. для всех номеров n начиная с номера .

Очевидно, что любая бесконечно большая последовательность является неограниченной.

Обратное утверждение неверно. Последовательность может быть неограниченной, но не быть бесконечно большой.

Пример 5. Доказать, что последовательность не является ограниченной, но и не является бесконечно большой.

То, что эта последовательность неограниченна следует из того, что она содержит сколь угодно большие элементы (на нечётных местах). Бесконечно большой эта последовательность не является. Это связано с тем, что все элементы с чётными номерами в этой последовательности равны нулю.

Докажем строго, что данная последовательность не является бесконечно большой, т. е. что

В качестве такого M можно выбрать в данном случае . Какой бы мы ни указали номер N всегда найдется номер (), такой, что . Этому условию удовлетворяет элемент с любым четным номером, большим N.

< Предыдущая		Следующая >