1.1. Последовательность. Способы задания последовательности

Def 1. Пусть – конечное или счетное числовое множество (не более, чем счетное), N – множество натуральных чисел. Если N поставлено в соответствие число , то говорят, что определена числовая последовательность

Числовую последовательность будем обозначать

Числа называют членами или элементами последовательности, – общим членом.

Числовая последовательность может быть задана с помощью формулы вида , выражающей через номер . Множество называется множеством значений последовательности.

Пример 1.

Формула , где и – некоторые вещественные числа определяет последовательность, которая называется геометрической прогрессией ( – знаменатель прогрессии) .

Пример 2.

Формула определяет арифметическую прогрессию ( – разность прогрессии) .

Для задания последовательности используют также рекуррентные формулы, т. е. формулы, выражающие n-тый член последовательности через члены последовательности с меньшими номерами.

Пример 3.

Последовательность Задана соотношением , , , т. е.

.

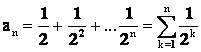Пример 4.

Последовательность чисел Фибоначчи задаётся рекуррентным соотношением 2-го порядка (связывающим с и )

, , . (1.1)

Зная это соотношение, можно получить формулу для вычисления в явном виде.

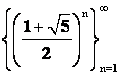Будем разыскивать последовательность , удовлетворяющую данному рекуррентному соотношению. Подставляя в соотношение (1.1), для определения получим квадратное уравнение , откуда следует, что существует, по крайней мере, две последовательности и , удовлетворяющие этому соотношению. Поскольку соотношение (1.1) однородное, то для любых постоянных и выражение также удовлетворяет соотношению (1.1). Константы и определяют из начальных условий: ; . Окончательно получаем .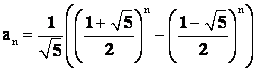

Последовательность, заданную рекуррентным соотношением , где N называют возвратной последовательностью порядка . Последовательность Фибоначчи является возвратной последовательностью второго порядка.

Множество , из которого строится последовательность (множество значений последовательности), может быть конечным, состоять, например, из двух элементов или даже одного элемента. Для последовательности множество состоит из двух элементов: , а для последовательности – из одного элемента: . Последовательности, множество значений которых состоит из одного элемента, называют стационарными.

< Предыдущая		Следующая >