06.5. Простейшие случаи криволинейной корреляции

В некоторых случаях ломаная, соединяющая точки, соответствующие парам значений Х и располагается вблизи кривой. Ограничимся рассмотрением корреляционной связи для двух простейших кривых: параболы, соответствующей трехчлену , и гиперболы, определяемой уравнением

1) Отыскание параметров квадратного трехчлена по способу наименьших квадратов с использованием данных простой таблицы значений Х и У подробно разобрано выше.

Если же значения Х и У представлены данными корреляционной таблицы, то корреляционная связь отыскивается как уравнение регрессии причем параметры этого уравнения определяются из системы нормальных уравнений, отражающих в структуре своих коэффициентов и свободных членов все данные корреляционной таблицы:

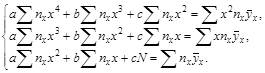
Заметим, что к выравниванию с помощью параболы второго порядка можно обращаться в тех случаях, когда использование линейной корреляции обнаруживает малую тесноту связи (значения коэффициента корреляции в границах 0,4 - 0,6).

В качестве примера применения способа наименьших квадратов для отыскания зависимости между У и Х в форме уравнения параболы второго порядка используем уже рассмотренные выше данные табл. 6 группировки 135 Сахаропесочных заводов по размеру основных производственных средств в млн. руб. (Х) и по среднесуточной переработке свеклы в тыс. Ц (У). ИСПользование этих данных для установления параболическоЙ корреляционной зависимости целесообразно в связи с отмЕЧенной выше малой теснотой линейной связи между рассматриваемыми показателями.

Для составления системы нормальных уравнений необходимые данные получаются суммированием, выполненным по схеме вспомогательной таблицы. Таблица 11

Х
1,75 2,25 2,75 3,25 3,75 4,25	21 42 25 24 13 10	36,75 94,50 68,75 78,00 48,75 42,50	64,31 212,63 189,06-253,50 182,81 180,63	112,55 478,38 520,00 823,92 685,49 767,70	196,97 1076,36 1430,00 2677,84 2570,28 3252,72	114 250 171 161 102 93	199,50 562,50 470,25 523,25 382,50 395,25	349,14 1139,06 1293,19 1700,56 1434,38 1679,81
	N=135	369,25	1082,94	3388,04	11204,17	891	2533,25	7596,14

По итоговым данным табл. 11 можно записать систему нормальных уравнений:

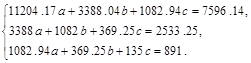
Решение этой системы дает параметры:

2) Рассмотрим корреляционную зависимость гипербОлического Типа, определяемую уравнением .

Пример 2. В табл. 12 дана группировка 44 предприятиЙ по выпуску продукции в тыс. Ед. (Х) и средней себестоимости единицы в руб. (У). Составить корреляционное уравнение связи этими показателями.

Х	До 1	1-2	2-3	3-4	4-5	5-6	6-7	7-8	8-9	9-10
Y	16,50	13,75	13,31	12,50	13,52	12,75	12,30	12,83	12,28	12,34
Число предприятий	6	6	8	7	4	4	3	2	2	2

Ломаная, отображающая данные этой таблицы (рис. 15), позволяет обратиться к уравнению гиперболы.

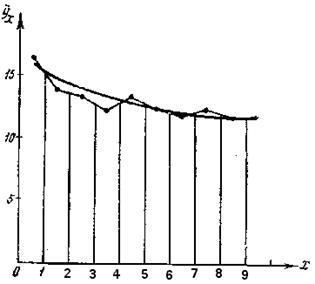
Рис. 15

Применим способ наименьших квадратов для определения парА метров искомого уравнения в виде .

Для функции необходимые условия минимума и приводят к системе

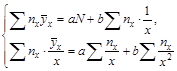
Суммирование выполняется на вспомогательной таблице (табл. 13)

Таблица 13

X
0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5	16.50 13.75 13.31 12.50 13.52 12.75 12.30 12.83 12. 28 12.34	6 6 8 7 4 4 3 2 2 2	12.000 4.000 3.200 2.000 0.888 0.728 0.462 0.266 0.236 0.210	24.000 2.664 1.280 0.574 0.196 0.132 0.072 0.036 0.028 0.022	99.00 82.50 100.48 87.50 54.08 51.00 36.90 25.66 24.56 24.68	198.000 55.000 40.192 24.100 12.178 9.273 5.677 3.421 2.889 2.591
		N=44	23,990	29,004	586,36	353,301

Система нормальных уравнений

Определяет параметры:

и

Отсюда искомое уравнение регрессии запишется так:

Соответствующая этому уравнению линия регрессии изображена вместе с ломаной на рис. 15.

Для иЗМерения тесноты связи при линейной корреляции введен Коэффициент корреляции. Общим измерителем тесноты связи для всех случаев корреляции как линейной, так и криволинейной служат Корреляционные отношения .

Рассмотрим корреляционное отношение для корреляционной зависимости, выражаемой уравнением , которое устанавливает связь между частными средними , и соответственными значениями Х.

В этом случае корреляционное отношение (его символ H) определяется формулой , которая выражает Отношение среднеГО Квадратического отклонения частных средних от общей средней у к среднему Квадратическому отклонению значений у от общей средней .

Аналогично вводится понятие о корреляционном отношении С соответствующей формулой

3ДЕсЬ означает среднее Квадратическое отклонение часТНых средних от общей средней , а — среднее квадратическое отклонение значений Х от .

Это отношение в случаях линейной корреляции оказывается не меньше коэффициента корреляции, в чем можно убедиться на данных примера.

Ранее был найден коэффициент корреляции по формуле

.

При определении корреляционного отношения из имеющихся данных для вычисления R используется значение . Следует определить еще . Но величина , выражающая дИСперсию частных средних значений , oпpeделяется в виде:

.

Здесь

Отсюда

И

Таким образом,

Ограничимся этим примером, опуская общий вывод того, что в случаях Линейной корреляции значение корреляционного отношения оказывается не меньше значения коэффициента корреляции, т. Е. что .

При этом знак равенства возможен только в случаях точной корреляционной связи:

при точной линейной корреляцИОнной связи У по Х

при точной линейной корреляционной связи X по Y

при точной линейной корреляционной связи У по Х, и X по Y.

< Предыдущая		Следующая >