06.6. Понятие о множественной корреляции
Этот вид корреляционной зависимости возникает в тех случаях, когда рассматривается связь между тремя или большим числом прИЗнаков, характеризующих изучаемое явление.
Ограничиваясь линейной корреляционной связью между величиной Z и аргументами Х и У, общий вид которой
![]() ,
,
Заметим, что эту связь выгодней рассматривать в форме зависимости между отклонениями величин Х, у И Z от их средних Х, у И Z. ЭТИм требуемая корреляционная зависимость приводится к виду
![]() .
.
Коэффициенты этого уравнения А и В выражают коэффициенты регрессии, которые опреДеЛяются по формулам:
![]() и
и ![]() .
.
Компонентами этих коэффициентов служат коэффициенты корреляции между Х и У ![]() , Х и Z
, Х и Z ![]() и Y и Z
и Y и Z ![]() , а также соответственные соотношения между средними Квадратическими Отклонениями величины Z и каждого аргумента (Х и У).
, а также соответственные соотношения между средними Квадратическими Отклонениями величины Z и каждого аргумента (Х и У).
Такая структура коэффициентов регрессии А и В показывает, что для составления линейного корреляционного уравнения между тремя величинами требуется предварительное вычисление трех коэффициентов корреляции — между аргументами Х и У, а также между каждым аргументом и величиной Z. Эти же коэффициенты корреляции используются в выражении сводного коэффициента корреляции, определяющего тесноту корреляционной связи между тремя величинами Х, у И z: 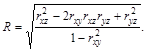
Этот коэффициент принимает значения ![]() . При R=0 линейная связь между Х, у, и z отсутствует, а при R=1 между ними имеется точная линейная связь
. При R=0 линейная связь между Х, у, и z отсутствует, а при R=1 между ними имеется точная линейная связь ![]()
Упражнения
1. Результаты медицинского обследования 100 мужчин по объему грудной клетки в см (Х) и общему росту (У) дали следующую таблицу:
|
X |
170 |
175 |
180 |
185 |
190 |
195 |
Итого |
|
75 85 95 105 115 125 135 145 |
1 3 |
2 6 4 1 1 |
13 11 1 3 |
5 4 2 5 |
8 5 4 3 1 |
2 2 7 1 1 |
3 13 22 26 10 20 4 2 |
|
Итого |
4 |
14 |
32 |
16 |
21 |
13 |
100 |
По данным этой таблицы составить уравнения прямых регрессии и вычислить коэффициент корреляции.
2. При обследовании 50 учеников 4-го класса получены следующие данные о росте и весе учащихся:
|
Вес(Кг) Рост (СМ) |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
125 126 127 128 129 130 131 132 133 |
1 1 |
2 2 1 |
4 3 2 |
1 5 4 2 |
1 5 5 1 |
1 2 3 1 |
1 1 1 |
По данным обследования определить коэффициент корреляции и составить уравнение регрессии, связывающие рост ученика и его вес.
Отв. R=0.87.
| < Предыдущая | Следующая > |
|---|