06.4. Упрошенный способ вычисления коэффициента корреляции

Выше в п. п. 6.2 и 6.3, при составлении уравнений прямых регрессии либо по данным корреляционной таблицы непосредственно вычислялись коэффициенты регрессии, либо по тем же данным предварительно вычислялся коэффициент корреляции. В обоих случаях вычисления были очень громоздкими (операции с многозначными числами).

Между тем при постоянных разностях для рассматриваемых в таблицах значений Х и У (в табл. 1 и , а в табл. 6 и ) можно заметно упростить вычисления, используя линейное преобразование переменных по формулам: и

Где и — произвольно выбираемые значения из заданных значений переменных Х И у, а и И V — Новые переменные.

Так, для рассматриваемых значений Х и У в табл. 1 можно провести преобразования

и ,

При которых соответствие между значениями Х И и, а также между Y и V отражено в табл. 8а и 8б.

Если же применяются преобразования

и ,

То получается другое соответствие (см. табл. 8в и 8г).

Таблица 8

А		Б		В		Г
Х	И		Y	V		X	U		Y	V
25 35 45 55 65 75 85 95 105 115 125	0 1 2 3 4 5 6 7 8 9 10		13 18 23 28 33 38 43 48 53 58 63 68	0 1 2 3 4 5 6 7 8 9 10 11		25 35 45 55 65 75 85 95 105 115 125	-5 -4 -3 -2 -1 0 1 2 3 4 5		13 18 23 28 33 38 43 48 53 58 63 68	-5 -4 -3 -2 -1 0 1 2 3 4 5 6

Преобразования второй серии обеспечивают большее упрощение вычислений, так как в этом случае все операции ведутся с меньшими по абсолютной величине числами.

Для обоснования этих линейных преобразований

и

Можно показать, что операции над переменными Х и У, связанные с вычислением коэффициента корреляции и коэффициентов регрессии, сводятся при этих преобразованиях к аналогичным операциям над новыми переменными И и V.

Прежде всего следует заметить, что средним значениям Х и У соответствуют средние значения переменных И и V:

Отсюда, при зависимосТИ будет и

Таким же образом можно установить, что

, или .

Далее, разность а поэтому

Аналогично устанавливается, что .

Эти результаты показывают, что участвующие в Вычислениях средние квадратические отклонения принимают вид и .

Наконец, преобразование разности Дает

.

Таким образом, переход к новым переменным дает преобразованную форму коэффициента корреляции и коэффициентов регрессии:

Для составления уравнений регрессии с помощью новых переменных следует включать в корреляционную таблицу значения этих новых переменных, найденные по формулам:

и .

Удобней всего применять для этой цели исходную таблицу, помещая в ней значения И слева от соответственных значении Х, а значения V — Над соответственными значениями У. При этом вспомогательный характер значений И и V в таблице обычно оттеняется применением для них мелкого шрифта.

Для иллюстрации тех упрощений, которые достигаюТСя введением новых переменных, используем этот способ на уже рассмотренном примере с распределением растений житняка. В виде значений и переменных Х и У выгодней всего используются их средние или ближайшие к ним значения этих переменных. В примере с растениями житняка именно такую замену представляют данные второго преобразования. Поставленные во вторых столбцах табл. 8в и 8г числа получены таким образом: для значений переменной И преобразованием

,

А для значений переменной V преобразованием

.

Вся операция по отыскаНИю параметров уравнений регрессии проводится по отдельным этапам.

1) Корреляционная таблица 1 пополняется значениями И и V.

2) Для отыскания коэффициента корреляциИ составляется Вспомогательная таблица (см. табл. 10) с вычислением ее Итоговых Данных.

Таблица 9

	V	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
U	Y X	13	18	23	28	33	38	43	48	53	58	63	68
-5	25	3	2	¾	¾	¾	¾	¾	¾	¾	¾	¾	¾	5
-4	35	¾	6	4	¾	¾	¾	¾	¾	¾	¾	¾	¾	10
-3	45	¾	1	13	5	¾	¾	¾	¾	¾	¾	¾	¾	19
-2	55	¾	1	2	4	8	1	¾	¾	¾	¾	¾	¾	16
-1	65	¾	¾	1	¾	4	4	2	¾	¾	¾	¾	¾	11
0	75	¾	¾	¾	¾	2	6	6	2	¾	¾	¾	¾	16
1	85	¾	¾	¾	¾	¾	¾	1	5	¾	¾	¾	¾	6
2	95	¾	¾	¾	¾	¾	¾	¾	1	4	1	¾	¾	6
3	105	¾	¾	¾	¾	¾	¾	¾	¾	2	4	1	1	8
4	115	¾	¾	¾	¾	¾	¾	¾	¾	¾	1	¾	1	2
5	125	¾	¾	¾	¾	¾	¾	¾	¾	¾	¾	¾	1	1
		3	10	20	9	14	11	9	8	6	6	1	3	100

3) По данным подсчетов:

Следует заметить, что , а таКжЕ что формулы преобразования и Позволяют: По найденным средним значениям новых переменных

и

Сразу получить средние значения старых переменных:

	U					V
5 10 19 16 11 16 6 6 8 2 1	-5 -4 -3 -2 -1 0 1 2 3 4 5	-25 -40 -57 -32 -11 0 6 12 24 8 5	125 160 171 64 11 0 6 24 72 32 25	-5(-23) = 115 -4(-36) = 144 -3(-53) = 159 -2(-26) = 52 -l(-5) = 5 0 1×11 = 11 2×18 = 36 3×33 = 99 4×10 = 40 5×6 = 30	3 10 20 9 14 11 9 8 6 6 1 3	-5 -4 -3 -2 0 1 2 3 4 5 6	-15 -40 -60 -18 -14 0 9 16 18 24 5 18	75 160 180 36 14 0 9 32 54 96 25 108
N = = 10					N = 100

Совпадение с данными о значениях и , найденных Непосредственным вычислением, подтверждает правильность проведения упрощенных вычислений.

4) Определив значения трех разностей: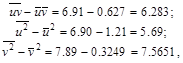

Можно записать, что и

Отсюда определяется коэффициент корреляциИ

Коэффициент регрессии У по Х

Коэффициент регрессии Х по У

Расхождения полученных коэффициентов с результатами непосредственных вычислений относятся к третьим десятичным знакам, что связано с приближенным характером вычислений.

< Предыдущая		Следующая >