06.3. Коэффициент корреляции
В рассмотренном примере корреляционной связИ оба коэффициента регрессии ![]() и
и ![]() положительны. В таком случае корреляцию называют положительной, что имеет место при изменении изучаемых количественных признаков в одинаковом направлении (Х и У одновременно возрастают или одновременно убывают).
положительны. В таком случае корреляцию называют положительной, что имеет место при изменении изучаемых количественных признаков в одинаковом направлении (Х и У одновременно возрастают или одновременно убывают).
Прямые при положительных коэффициентах регрессии обраЗУют острые углы с соответствующими осями координат (рис. 14) — у прямой регрессии У по Х коэффициент регрессии ![]() , где A — острый угол, образованный прямой I с осью Ох, а у прямой регрессии Х по Y коэффициент регрессии
, где A — острый угол, образованный прямой I с осью Ох, а у прямой регрессии Х по Y коэффициент регрессии ![]() , Где B — острый угол, образованный прямой II с осью Оу. При отрицательных коэффициентах регрессии прямые регрессии образуют с соответствующими осями тупые углы.
, Где B — острый угол, образованный прямой II с осью Оу. При отрицательных коэффициентах регрессии прямые регрессии образуют с соответствующими осями тупые углы.
ДЛЯ большей наглядности на рис. 14 показано положение прямых регрессии относительно новой системы координат с началом в точке ![]() пересечения этих прямых.
пересечения этих прямых.
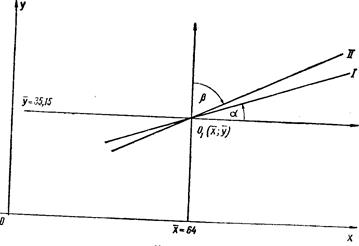
Рис. 14
Сами по себе значения коэффициентов регрессии не поЗВоляют судить о тесноте связи между Х и У. Это зависит от величины угла, образованного прямыми регрессии. Чем меньше этот угол, теЛ; Теснее корреляционная связь между Х и У.
При слиянии этих двух прямых в одну имеет место линейная функциональная зависимость между Х и У.
В качестве меры тесноты линейной корреляционной связИ прИНимаетСЯ коэффициент корреляции
![]()
Со знаком, совпадающим со знаками коэффициентов регрессии. При этом, если прямые I и II совпадают, то ![]() и
и ![]() . Но тогда
. Но тогда ![]() и, следовательно,
и, следовательно, ![]() .
.
Обращение коэффициента корреляции в 1 или в -1 является, как это можно доказать, Необходимым и достаточным признаком. линейной функциональной зависимости между х и У.
Корреляционная таблица в таких случаях состоит из расположенных лишь на одной диагонали частот значений Х и У.
Вместе с тем, когда, по крайней мере, один из углов A или B равен нулю, то и ![]() , а значит, и между рассматриваемыми величинами не существует ни функциональной, ни корреляционной линейной зависимости. Однако в этом случае между Х и У возможны нелинейные корреляционные и даже функциональные связи.
, а значит, и между рассматриваемыми величинами не существует ни функциональной, ни корреляционной линейной зависимости. Однако в этом случае между Х и У возможны нелинейные корреляционные и даже функциональные связи.
Корреляционная зависимость между Х и У (для положительных коэффициентов регрессии) ИМеет место, когда коэффициент корреляциИ, как это можно доказать, выражается правильной дробью (0 < R < 1). При этом связЬ между переменными тем теснее, чем ближе коэффициент корреляции к 1.
Введенное определение коэффициента корреляции в виде ![]() позволяет на основании выражений коэффИЦиентов регрессии получить удобную формулу для непосредственного вычисления коэффициента корреляции.
позволяет на основании выражений коэффИЦиентов регрессии получить удобную формулу для непосредственного вычисления коэффициента корреляции.
Если обратитЬСя к выражениям коэффициентов прямых регРЕссии
![]() и
и ![]() ,
,
То можно ЗАметить, что знаменатели в обоих Выражениях обозначают ДисперсиИ соответствующих рядов распределений:
![]() и
и ![]() .
.
Отсюда можно получить для коэффициента КорРеляции формулу
![]() ,
,
Которая сразу показывает, что между независимыми величинами корреляции не существует, так как для таких величин выполняется равенство ![]() .
.
Замечание. Последнее равенство является приближенным, а поэтому если коэффициент корреляции очень мал ![]() , считают, что линейной коррЕЛяции между Х и У нет.
, считают, что линейной коррЕЛяции между Х и У нет.
Записанная выше формула позволяет выразить каждый коэффициент регрессии через коэффициент корреляции.
Так, коэффициент регрессии У по X
![]() ,
,
А коэффициент регрессии Х по У
![]() .
.
Такие выражения коэффициентов регрессии показывают, что составление уравнений прямых регрессии может быть облегчено, если будет найдено значение коэффициента корреляции. Для его вычисления следует использовать выражения числителя и знаменателя:
![]() .
.
Тогда можно вычислить коэффициент корреляции по формуле
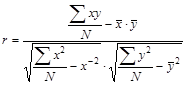 .
.
Пример 1. В табл. 6 дана группировка 135 Сахаропесочных Заводов по размеру производственных основных средств в млн. руб. (Х) и по среднесуточной переработке свеклы в тыс. Ц (У). Требуется определить коэффициент корреляции и составить уравнеНИя регрессии.
Таблица 6
|
X |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 | |
|
1,75 2,25 2,75 3,25 3,75 4,25 |
4 5 ¾ 3 ¾ ¾ |
6 9 4 3 ¾ ¾ |
9 15 6 2 3 ¾ |
2 10 7 7 3 2 |
¾ 2 7 8 2 2 |
¾ 1 1 3 1 |
¾ ¾ 1 2 2 |
¾ ¾ ¾ ¾ ¾ 2 |
¾ ¾ ¾ ¾ ¾ 1 |
21 42 25 24 13 10 |
|
|
12 |
22 |
35 |
31 |
21 |
6 |
5 |
2 |
1 |
135 |
Расположение рядов распределения значений У в табл. 6 позволяет наметить линейную корреляционную связь между Х и У.
Для отыскания коэффициента корреляции составим вспомогательную таблицу.
Таблица 7
|
|
| ||||||
|
21 42 25 24 13 10 |
21×1,75 42×2,25 25×2,75 24×3,25 13×3,75 10×4,25 |
21×3,0625 42×5,0625 25×7,5625 24×10,5625 13×14,0625 10×18,0625 |
1,75×114 2,25×250 2,75×171 3,25×161 3,75×102 4,25×93 |
12 22 35 31 21 6 5 2 1 |
12×4 22×5 35×6 31×7 21×8 6×9 5×10 2×11 1×12 |
12×16 22×25 35×36 31×49 21×64 6×81 5×100 2×121 1×144 |
4×28,00 4×51,50 6×83,75 7×87,75 8×65,75 9×21,00 10×18,75 11×8,50 12×4,25 |
|
N=135 |
369,25 |
1082,9375 |
2533,25 |
135 |
891 |
6237 |
2533,25 |
Следует пояснить, что вторые множители в четвертом столбце ![]() получены из данных табл. 6 суммированием произведений каждого числа внутренней строки на соответствующее значение У (например, 114=4×4+6×5+9×6+2×7; 171= 4×5+6×6+7×7+8×7+1×10).
получены из данных табл. 6 суммированием произведений каждого числа внутренней строки на соответствующее значение У (например, 114=4×4+6×5+9×6+2×7; 171= 4×5+6×6+7×7+8×7+1×10).
Так как суммирование этих вторых множителей ДаЕт сумму всех значений У, то сумма ![]() , и это равенство подтверЖДает правильность подсчета суммы всех значений У. Аналогична структура вторых множителей в последнем столбце. Например, 28 = 4×1,75+5×2,25+3×3,25. Здесь суммирование вторых множителей дает сумму всех значений Х, а потому РАвеНСТВо
, и это равенство подтверЖДает правильность подсчета суммы всех значений У. Аналогична структура вторых множителей в последнем столбце. Например, 28 = 4×1,75+5×2,25+3×3,25. Здесь суммирование вторых множителей дает сумму всех значений Х, а потому РАвеНСТВо ![]() Служит для подтверждения правильности подсчета. Вместе с тем итоговые суммы по четвертому и последнему столбцам являются в то же время суммами всех участвующих в таблиЦЕ парНЫх Произведений Ху. Отсюда
Служит для подтверждения правильности подсчета. Вместе с тем итоговые суммы по четвертому и последнему столбцам являются в то же время суммами всех участвующих в таблиЦЕ парНЫх Произведений Ху. Отсюда ![]() .
.
По данным подсчетов имеем:
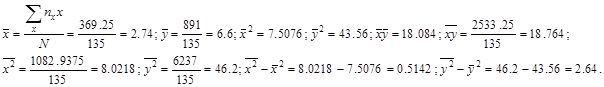
Отсюда ![]() и
и ![]() И коэффициент корреляции
И коэффициент корреляции
![]() .
.
Для составления уравнений прямых регрессии Определяем коэффициенты регрессии:
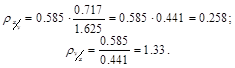
Таким образом, уравнение прямой регрессии У по Х
![]() или
или ![]()
А уравнение прямой регрессии Х по У
![]() или
или ![]()
Сравнение коэффициента корреляции в этом примере ![]() с коэффициентом корреляции в ранее рассмотренном примере расПределения растений житняка
с коэффициентом корреляции в ранее рассмотренном примере расПределения растений житняка
![]()
Показывает на большую тесноту связи между, общим весом и весом семян. Это согласуется со структурой соответствуюЩИх корреляциОнных таблиц. Табл. 1 распределения растений житняка характерна четким смещением рядов распределения значений У при малой степени рассеяния этих значений, а табл. 6 по Сахаропесочным заводам дает малозаметное смещение рядов распределения значений У при значительной степени рассеяния этих значений.
| < Предыдущая | Следующая > |
|---|