06.2. Линейная корреляция
Этот вид корреляционной зависимости весьма важен, так как очень многие корреляционные связи, характерные для количественных признаков наблюдаемых однородных фактов, близки к линейным. Данные наблюдения, представленные в виде корреляционной таблицы, и найденные из этой таблицы пары соответственных значений Х и 
или У и 
, используются для отыскания параметров уравнений прямых регрессии
и 
.
Эта операция, называемая Выравниванием, обычно выполняется по способу наименьших квадратов, сущность которого состоит в таком подборе параметров линии регресси, при котором достигается минимум 
.
Разберем применение данного способа в общем виде для каждого из записанных уравнений регрессии. При этом для иллюстрации используем данные корреляционной таблицы 1 распределения растений житняка по общему весу и по весу семян.
1. УравнеНИе прямой регрессии У по х. При отыскании по способу наименьших квадратов параметров линейной функции У=ах+B На основании данных наблюдения о парах значений Х и У, связанных однозначным соответствием, используется система нормальных уравнений
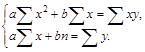
Здесь коэффициенты определяются простым суммированием слагаемых в соответствии с количеством пар значений Х и У.
Если же требуется с помощью способа наименьших квадратов определить параметры уравнения, связывающего значения Х с соответственными частными средними , по данным не простой, а корреляционной таблицы, то структура коэффициентов и свободных членов нормальных уравнений должна отразить все данные корреляционной таблицы.
А) Коэффициенты, соответствующие суммам 
и 
, должны включать в операцию суммирования все значения Х как повторяющиеся, так и неповторяющиеся. Количество значений 
определяется числом 
, поэтому сумма этих значений Х равна 
. Аналогично сумма значений 
равна 
и т. Д. Отсюда сумма всех значений Х выразится в виде
Суммирование квадратов переменной Х строится также и дает
Б) Свободный член, сооТВеТСтвуЮщИй сумме 
, должен представить сумму всех частных средних . При этом для каждого значения Х количество соответственных частных средних определяется количеством таких значений самого Х. Поэтому значению соответствует , частных средних 
, значенИЮ Соответствует 
частных средних 
и т. д. Сумма всех частных средних Имеет вид
.
В) Свободный член, соответствующий сумме 
, должен представить сумму всех воЗМожных произведений значений Х на соответствующие частные срЕДние . КоличестВО разных произведений здесь определяется количеством соответственных значений Х. Поэтому сумма всех произведений вида 
имеет вид
.Удовлетворяющая указанным требованиям система нормальных уравнений для отыскания значений параметров уравнения прямой регрессии имеет следующий вид:
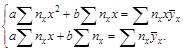
Определение корней этой системы предварительно требует некоторого преобразования коэффициентов и свободных членов.
Коэффициенты системы преобразуются так:
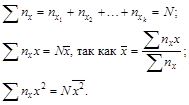
Развернутая запись свободного члена 
позволяет для каждого слагаемого воспользоваться переходом от частных средних к соответственным частным значениям У.
В самом деле, если , то
.
Поэтому
И аналогично
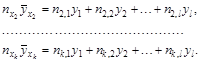
Почленное сложЕНие всех равеНСтв дает в СОответствии с ПРинятой структурой корреляционной таблицы 2
После приведения этого результата к выражению, Содержащему среднее значение У, получится
.
Преобразование свободного члена 
выполняется Аналогично. Здесь При слагаемое 
приводится к виду 
Последующая запись всех остальных слагаемых такого же вИДа при , 
и суммирование соответствующих выражений дает реЗУльтаТ 
Сохраняя эту запись для выполнения подсчетов, можно привести полученный результат к выражению со средним значением Ху.
Двойной знак суммирования позволяет выполнять суммирование в любом порядке: сНАчала по горизонтали (меняя нумерацию частных значений У), а ЗАтем по вертикали (меняя нумерацию частных значений Х), или, наоборот, сначала по вертикали, а затем по горизонтали.
По структуре корреляционной таблицы: 
Или 
Отсюда 
Так как 
В преобразованном виде система такова: 
Или 
Для определения параметра A достаточно после умножения членов второго уравнения на 
почленно вычесть это уравнение из первого: 
, или 
Параметр B определяется непосредственно из второго уРАвНенИя:
.
Подставляя полученное выражение в уравнение прямой регрессии Y по Х, т. Е. , получим
,Или 
.
КоэффИЦиент А в уравнении прямой регрессии называется КоЭФфициентом прямой регрессии у по х И обозначается символом 
.
Таким образом, 
И окончательная запись уравнения прямой регрессии Y по X таково:
.
Составим такое уравнение с числовыми параметрами для распределения растений житняка по данным корреляционной таблицы 1 об общем весе (X) и весе семян (Y) растений. Вычисление необходимых параметров можно проводить по нижеследующей системе поДСчетов, соответствующей выполненному общему решению.
1) Составляем вспомогательную таблицу.
2) По данным табл. 4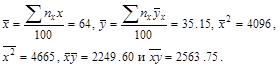 
Таблица 4
|
|
|
|
| |
|
5 |
5×25 |
75 |
5×625 |
1875 |
|
10 |
10×35 |
200 |
10×1225 |
7000 |
|
19 |
19×45 |
457 |
19×2025 |
20565 |
|
16 |
16×55 |
478 |
16×3025 |
26290 |
|
11 |
11×65 |
393 |
11×4225 |
25545 |
|
16 |
16×75 |
648 |
16×5625 |
48600 |
|
6 |
6×85 |
283 |
6×7225 |
24055 |
|
6 |
6×95 |
318 |
6×9025 |
30210 |
|
8 |
8×105 |
469 |
8×11025 |
49245 |
|
2 |
2×115 |
126 |
2×13225 |
14490 |
|
1 |
1×125 |
68 |
1×15625 |
8500 |
|
N=100 |
6400 |
3515 |
466500 |
256375 |
3) Определяем коэффициент регрессии У по Х:
4) Записываем уравнение прямой регрессии У по X:
,Или окончательно 
2. Уравнение прямой регрессии Х по У. Система нормальных уравнений для отыскания параметров С и D уравнения прямой регрессии Х по У, получаемая в результате применения способа наименьших квадратов, имеет вид
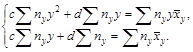
По аналогии с преобразованиями, проведенными для случая регрессии У по Х, можно записать, что
Нормальные уравнения можно переписать в упрощенном вИДе:
Или 
Для определения параметра С из членов первого уравнЕнИя вЫЧитаются члены второго уравнения, умноженные на 
:
,
Или 
Параметр D определяется непосредственно из второго уравнения:
.
Замена D этим выражением в уравнении прямой регрессии дает
Или 
.
Коэффициент С в этом уравнении называют Коэффициентом прямой Регрессии х по у И обозначают символом 
.
Таким образом, 
И окончательная запись уравнения прямой регрессии Х по У такова:
.
Заметим, что обе прямые регрессии, как видно из их уравнений, проходят через точку 
.
На примере распределения растений житняка по данным корреляционной таблицы о весе семян (У) и общем весе (Х) растений составим уравнение прямой регрессии Х по У с числовыми параметрами. Все необходимые вычисления для подсчета параметров проводятся в таком же порядке, как это выполнено для уравнения прямой регрессии У по Х.
1) Составляем вспомогательную таблицу.
3) Определяем коэффициент регрессии Х по У:
Таблица 5
|
|
|
|
| |
|
3 |
3×13 |
75 |
3×169 |
975 |
|
10 |
10×18 |
360 |
10×324 |
6480 |
|
20 |
20×23 |
900 |
20×529 |
20700 |
|
9 |
9×28 |
445 |
9×784 |
12460 |
|
14 |
14×33 |
850 |
14×1089 |
28050 |
|
11 |
11×38 |
765 |
11×1444 |
29070 |
|
9 |
9×43 |
665 |
9×1849 |
28595 |
|
8 |
8×48 |
670 |
8×2304 |
32160 |
|
6 |
6×53 |
590 |
6×2809 |
31270 |
|
6 |
6×58 |
630 |
6×3364 |
36540 |
|
1 |
1×63 |
105 |
1×3969 |
6615 |
|
3 |
3×68 |
345 |
3×4624 |
23460 |
|
N=100 |
3515 |
6400 |
142465 |
256375 |
4) Записываем уравнение прямой регрессии Х по Y:
,
Или окончательно 
Ниже будет показано, что оба уравнения прямых регрессии могут быть получены одним расчетом с помощью коэффициента корреляции.
| < Предыдущая | Следующая > |
|---|
