33.2. Основная модель управления запасами

Введем обозначения необходимых для составления модели величин. Данные поместим в табл. 33.1.

График изменения запасов представлен на рис. 33.2.

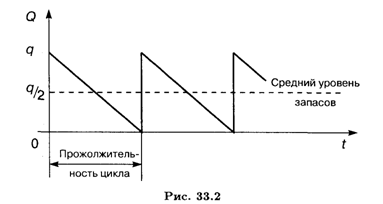
Чтобы полностью удовлетворить годовой спрос G при раз­мере поставки Q, необходимо обеспечить G/Q поставок или пар­тий за год. Средний уровень запасов составляет Q/2.

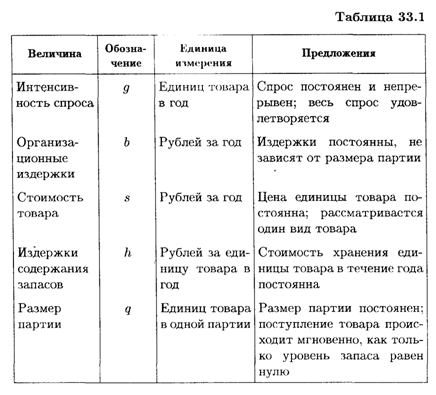
Уравнение издержек будет иметь вид

Где С1 — общие организационные издержки; С2 — стоимость товаров; С3 — общие издержки содержания запасов.

За исключением Q все величины в правой части уравнения постоянны и известны, т. е. С = F(Q). Для нахождения мини­мума С найдем производную DC/Dq и приравняем ее к нулю:

Откуда

Где QОпт — оптимальный размер партии.

Иногда возникает соблазн заказывать размер партии то­варов, не соответствующий оптимальному размеру. Это при­водит к увеличению издержек на содержание и организацию поставок. Покажем, что это так.

Предположим, что вместо оптимального размера была за­казана партия товаров, равная 0,5 QОпт. Из основного уравнения издержек

Найдем

В случае заказа 0,5 QОпт получим

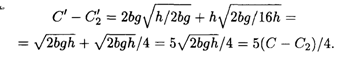
Таким образом, заказ партии товаров размером 0,5 QОпт (вместо QОпт) приводит к увеличению общих издержек на со­держание запасов и организацию поставок на 25%. Аналогич­ная картина наблюдается в случае заказа поставок больше чем QОпт.

Изобразим графически (рис. 33.3) изменение отдельных со­ставляющих величин С.

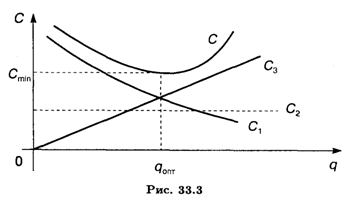
Из рис. 33.3 следует, что увеличение Q ведет к резкому сни­жению C1, при этом С3 увеличивается пропорционально H/2. При малых значениях Q величина С падает до значения СMin в точке QОпт. При увеличении Q величина издержек С прибли­жается к С2 + С3.

< Предыдущая		Следующая >