31.2. Решение игр (Aij)MXN с помощью линейного программирования

Теория игр находится в тесной связи с линейным програм­мированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного про­граммирования и решена симплексным методом и, наоборот, задача линейного программирования может быть представле­на как игра.

Для первого игрока математическая модель задачи запи­сывается в виде

При ограничениях:

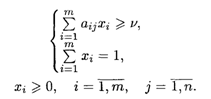
Математическую модель можно упростить, разделив все (П + 1) ограничений на V. Это возможно при V ≠ 0. При V = 0 рекомендуется прибавить любое положительное число ко всем элементам платежной матрицы, что гарантирует положи­тельность значения модифицированной игры. Действительное значение игры получается вычитанием из модифицированного значения этого положительного числа. Если V < 0, то надо сме­нить знаки неравенств. Полагая V > 0, систему ограничений можно записать так:

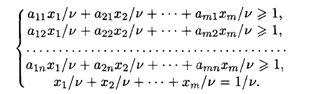
Положим Хi = xi/v. Так как V → max, то 1 / V → min. Получим задачу линейного программирования вида

При ограничениях:

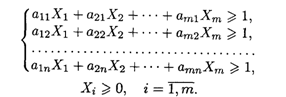
Для второго игрока математическая модель записывается в виде

При ограничениях:

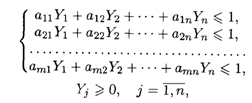
Где S() = 1 / V, Yj = УJ / v.

Задача второго игрока является двойственной по отноше­нию к задаче первого игрока. Можно найти решение одного из игроков, а затем по теоремам двойственности — решение другого.

< Предыдущая		Следующая >