31.1. Графическое решение игр вида (2 x N) и (M x 2)

Графический метод применим к играм, в которых хотя бы один игрок имеет только две стратегии. Рассмотрим игру (2 х П), см. табл. 31.2.

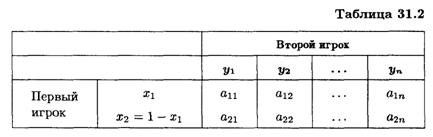
Предполагаем, что игра не имеет седловой точки.

Обозначим: Х1 — вероятность применения первым игроком 1-й стратегии, X2 — вероятность применения первым игроком 2-й стратегии, причем Х2 = 1 — X1; Y1 — вероятность примене­ния вторым игроком 1-й стратегии, У2 — вероятность приме­нения вторым игроком 2-й стратегии и т. д., УN — вероятность применения вторым игроком П-й стратегии.

Ожидаемый выигрыш первого игрока при применении вто­рым 1-й стратегии составит

Аналогично найдем ожидаемые выигрыши первого игрока при применении вторым игроком 2, 3, ..., N-й стратегий. Полу­ченные данные поместим в табл. 31.3.

Из таблицы видно, что ожидаемый выигрыш первого иг­рока линейно зависит от X1. На оси X1 построим выражения ожидаемых выигрышей первого игрока.

Первый игрок должен выбирать такие стратегии, чтобы максимизировать свой минимальный ожидаемый выигрыш. Поэтому оптимальная стратегия первого игрока определяется как точка пересечения прямых, максимизирующих его мини­мальный ожидаемый выигрыш.

Аналогично находим оптимальную стратегию второго иг­рока. Она определяется как точка пересечения прямых, мини­мизирующих его максимальные ожидаемые проигрыши.

Пример 1. Рассмотрим представленную выше игру, заданную платежной матрицей

Найти оптимальные стратегии игроков и цену игры.

Решение. Обозначим: X1 — вероятность применения пер­вым игроком 1-й стратегии, Х2, х3, х4 — вероятность исполь­зования первым игроком 2, 3, 4-й стратегий соответственно, причем Х1 + X2 + X3 + X4 = 1; Y1 — вероятность применения вторым игроком 1-й стратегии, У2, у3, Y4, Y5 — вероятность использования вторым игроком 2, 3, 4, 5-й стратегий соответ­ственно, причем Y1 + У2 + У3 + y4 + y5 = 1.

Платежная матрица была упрощена путем вычеркивания дублирующих, заведомо невыгодных стратегий. Поэтому X2 = X4 = Y1 = Y2 = y3 = 0 и матрица имеет вид

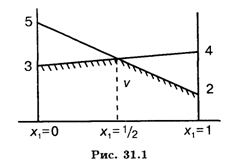
Найдем решение игры (табл. 31.4) графическим методом (рис. 31.1). На оси Х1 разместим точки Х1 = 0 и Х1 = 1, через которые проведем прямые, перпендикулярные оси Х1. Подстав­ляя Х1 = 0 и X1 = 1 в выражение Х1 +3, найдем значения, кото­рые отложим на соответствующих перпендикулярных прямых. Соединив эти точки, получим прямую.

Аналогично рассмотрим выражение –3X1 + 5.

Оптимальная стратегия первого игрока определится из ра­венства выражений Х1 + 3 и -3Х1 + 5:

Цена игры V = X1 + 3 = 1/2 + 3 = 7/2.

Оптимальная стратегия первого игрока:

Найдем оптимальную стратегию для второго игрока (табл. 31.5).

Имеем

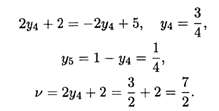
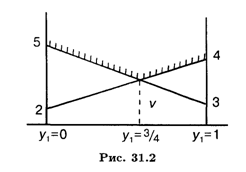
Оптимальная стратегия второго игрока (рис. 31.2):

Пример 2. Найдем решение игры вида (2 х N), заданной пла­тежной матрицей (табл. 31.6)

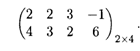
Решение. Находим

α = mах (-1,2) = 2, β = min (4, 3, 3, 6) = 3, 2 ≤ V ≤ 3.

Тогда

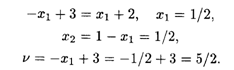
Оптимальное решение первого игрока:

Опт = (1/2, 1/2), при этом цена игры составляет V = 5/2.

Найдем оптимальное решение второго игрока (табл. 31.7).

Из рис. 31.3 следует, что оптимальная стратегия первого игрока определяется из равенства выражений –X1 + 3 и Х1 + 2, соответствующих 2-й и 3-й чистым стратегиям второго игрока (см. табл. 31.5), поэтому Y1 = Y4 = 0, а У3 = 1 – Y2.

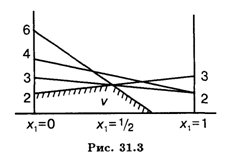
Имеем

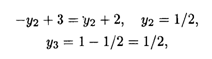
Откуда

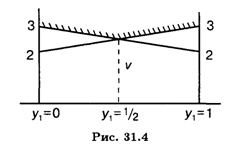
Оптимальное решение второго игрока (рис. 31.4):

Опт = (0,1 / 2,1 / 2,0), при этом цена игры V = 5/2.

Ответ.

Опт = (1/2, 1/2), Опт = (0,1 / 2,1 / 2,0), V = 5/2.

Пример 3. Найдем решение игры вида (т х 2), заданной пла­тежной матрицей (табл. 31.8)

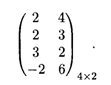
Решение. Находим α = mах (2, 2, 2, -2) = 2, β = min (3, 6) = 3, 2 ≤ V ≤ 3. Пусть Y1 и У2 (причем Y2 = l —Y1) — смешанные стратегии второго игрока; X1, X2, X3, X4 — смешанные страте­гии первого игрока.

Находим

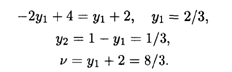
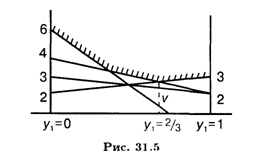
Оптимальное решение второго игрока (рис. 31.5):

Опт = (2/3, 1/3), при этом цена игры V = 8/3.

Прямые, пересекающиеся в минимаксной точке, соответ­ствуют 1-й и 3-й чистым стратегиям первого игрока. Это озна­чает, что Х2= х4 = 0. Следовательно, Х1 = 1 — X3. Найдем оптимальную стратегию 1-го игрока (табл. 31.9, рис. 31.6).

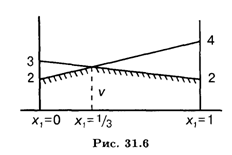
Имеем

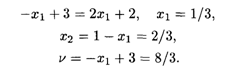
Оптимальное решение первого игрока:

Опт = (1/3, 0, 2/3, 0), при этом цена игры V = 8/3.

Ответ.

Опт = (1/3, 0, 2/3, 0), Опт = (2/3, 1/3), V = 8/3.

< Предыдущая		Следующая >