29.2.5. Нахождение рациональных затрат при строительстве трубопроводов и транспортных артерий

Требуется проложить путь (трубопровод, шоссе) между двумя пунктами А И В таким образом, чтобы суммарные за­траты на его сооружение были минимальные.

Решение. Разделим расстояние между пунктами А и В на шаги (отрезки). На каждом шаге можем двигаться либо строго на восток (по оси X), либо строго на север (по оси Y). Тогда путь от А в В представляет ступенчатую ломаную линию, от­резки которой параллельны одной из координатных осей. За­траты на сооружение каждого из отрезков известны (рис. 29.2) в млн р.

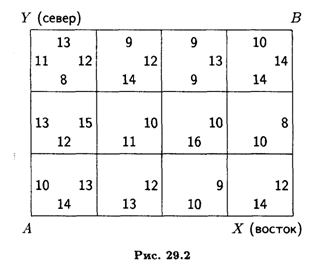
Разделим расстояние от А до В в восточном направлении на 4 части, в северном – на 3 части. Путь можно рассматри­вать как управляемую систему, перемещающуюся под влияни­ем управления из начального состояния А в конечное В. Со­стояние этой системы перед началом каждого шага будет характеризоваться двумя целочисленными координатами Х и У. Для каждого из состояний системы (узловой точки) найдем условное оптимальное управление. Оно выбирается так, что­бы стоимость всех оставшихся шагов до конца процесса была минимальна. Процедуру условной оптимизации проводим в об­ратном направлении, т. е. от точки В к точке А.

Найдем условную оптимизацию последнего шага (рис. 29.3).

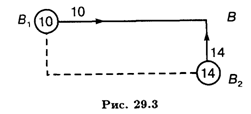
В точку В можно попасть из B1 или В2. В узлах запишем стоимость пути. Стрелкой покажем минимальный путь.

Рассмотрим предпоследний шаг (рис. 29.4).

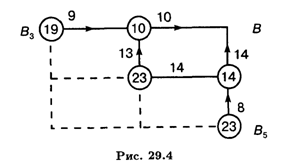
Для точки В3 условное управление — по оси X, а для точки B5 — по оси Y. Управление для точки В4 выбираем как

Т. е. по оси Y.

Условную оптимизацию проводим для всех остальных уз­ловых точек (рис. 29.5).

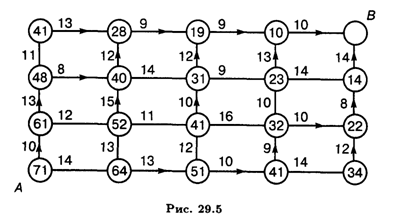
Получим

Где С — север, В —Восток.

Минимальные затраты составляют

Если решать задачу исходя из оптимальности на каждом этапе, то решение будет следующим:

Затраты составят 10 +12 + 11 + 10 + 9 + 13 +10 = 75 > 71.

Ответ. Прокладывать путь целесообразно по схеме: С, с, в, с, в, в, в, при этом затраты будут минимальные и составят 71 млн р.

< Предыдущая		Следующая >