29.2.4. Минимизация затрат на строительство и эксплуатацию предприятий

Задача по оптимальному размещению производственных предприятий может быть сведена к задаче распределения ре­сурсов согласно критерию минимизации с учетом условий целочисленности, накладываемых на переменные.

Пусть задана потребность в пользующемся спросом про­дукте на определенной территории. Известны пункты, в ко­торых можно построить предприятия, выпускающие данный продукт. Подсчитаны затраты на строительство и эксплуата­цию таких предприятий.

Необходимо так разместить предприятия, чтобы затраты на их строительство и эксплуатацию были минимальные.

Введем обозначения:

Х — количество распределяемого ресурса, которое можно использовать П различными способами,

Xi — количество ресурса, используемого по I-му способу (I = );

Gi(xi) — функция расходов, равная, например, величине за­трат на производство при использовании ресурса Xi по I-му способу;

φk(X) — наименьшие затраты, которые нужно произвести при использовании ресурса Х первыми K способами.

Необходимо минимизировать общую величину затрат при освоении ресурса X всеми способами:

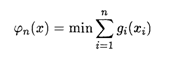
При ограничениях

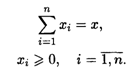
Экономический смысл переменных Xi состоит в нахождении количества предприятий, рекомендуемого для строительства в I-М пункте. Для удобства расчетов будем считать, что пла­нируется строительство предприятий одинаковой мощности.

Рассмотрим конкретную задачу по размещению предприя­тий.

Пример. В трех районах города предприниматель планирует построить пять предприятий одинаковой мощности по выпуску хлебобулочных изделий, пользующихся спросом.

Необходимо разместить предприятия таким образом, что­бы обеспечить минимальные суммарные затраты на их строи­тельство и эксплуатацию. Значения функции затрат Gi(X) при­ведены в табл. 29.4.

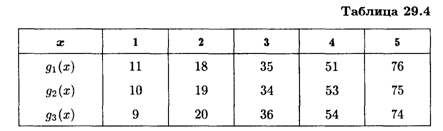
В данном примере Gi(х) — функция расходов в млн р., ха­рактеризующая величину затрат на строительство и эксплуа­тацию в зависимости от количества размещаемых предприя­тий в I-м районе;

φk(X) — наименьшая величина затрат в млн. р., которые нужно произвести при строительстве и эксплуатации предпри­ятий в первых K районах.

Решение. Решение задачи проводим с использованием ре­куррентных соотношений: для первого района

Для остальных районов

Задачу будем решать в три этапа.

1-й этап. Если все предприятия построить только в пер­вом районе, то

Минимально возможные затраты при Х = 5 составляют 76 млн р.

2-й этап. Определим оптимальную стратегию при разме­щении предприятий только в первых двух районах по формуле

Найдем φ2(l):

G2(1) + φ1(0) = 10 + 0 = 10,

G2(0) + φ1(l)= 0 +11 = 11,

φ2(l) = min (10, 11) = 10.

Вычислим φ2(2):

G2(2) + φ1(0) = 19 + 0 = 19,

G2(l) + φ1(l) = 10 + 11 = 21,

G2(0) + φ1 (2) = 0 + 18 = 18,

φ2(2) = min (19, 21, 18) = 18.

Найдем φ2(3):

G2(3) + φ1 (0) = 34 + 0 = 34,

G2(2) + φ1(l) = 19 + 11 = 30,

G2(1) + φ1(2) = 10 + 18 = 28,

G2(0) + φ1(3) = 0 + 35 = 35,

φ2(3) = min (34, 30, 28, 35) = 28.

Определим φ2(4):

G2(4) + φ1(0) = 53 + 0 = 53,

G2(3) + φ1(l) = 34 + 11 = 45,

G2(2) + φ1(2) = 19 + 18 = 37,

G2(l) + φ1(3) = 10 + 35 = 45,

G2(0) +φ1(4) = 0 + 51 = 51,

φ2(4) = min (53, 45, 37, 45, 51) = 37.

Вычислим φ2(5):

G2(5) + φ1(0) = 75 + 0 = 75,

G2(4) + φ1(l) = 53 + 11 = 64,

G2(3) + φ1(2) = 34 + 18 = 52,

G2(2) + φ1(3) = 19 + 35 = 54,

G2(1) + φ1(4) = 10 + 51 = 61,

G2(0) + φ1(5) = 0 + 76 = 76,

φ2(5) = min (75, 64, 52, 54, 61, 76) = 52.

3-й этап. Определим оптимальную стратегию при раз­мещении пяти предприятий в трех районах по формуле

φ3(X) = min{G3(X3) + φ2(X – х3)}.

Найдем φ3(5):

G3(5) + φ2(0) = 74 + 0 = 74,

G3(4) + φ2(1) = 54 + 10 = 64,

G3(3) + φ2(2) = 36 + 18 = 54,

G3(2) +φ2(3) = 20 + 28 = 48,

G3(1) + φ2(4) = 9 + 37 = 46,

G3(0) + φ2(5) = 0 + 52 = 52,

φ3(5) = min (74, 64, 54, 48, 46, 52) = 46.

Минимально возможные затраты при Х = 5 составляют 46 млн р.

Определены затраты на строительство предприятий от 1-го до 3-го этапа. Вернемся 3-го к 1-му этапу. Минимальные затраты в 46 млн р. на 3-м этапе получены как 9 + 37, т. е. 9 млн р. соответствуют строительству одного предприятия в третьем районе (см. табл. 29.4). Согласно 2-му этапу 37 млн р. получены как 19 + 18, т. е. 19 млн р. соответствуют строитель­ству двух предприятий во втором районе. Согласно 1-му этапу 18 млн р. соответствуют строительству двух предприятий в первом районе.

Ответ. Оптимальная стратегия состоит в строительстве одного предприятия в третьем районе, по два предприятия во втором и первом районах, при этом минимальная стоимость строительства и эксплуатации составит 46 ден. ед.

< Предыдущая		Следующая >