28.4.2. Расчет экономико-математической модели при нелинейных реализациях продукции

Рассмотрим применение выше приведенных методов на примере решения задачи оптимальной реализации продукции.

Пример 9. Мукомольный комбинат реализует муку двумя способами: в розницу через магазин и оптом через торговых агентов. При продаже X1 кг муки через магазин расходы на реализацию составляют Х12 ден. ед., а при продаже X2 кг муки посредством торговых агентов — Х22 ден. ед.

Определить, сколько килограммов муки следует продавать каждым способом, чтобы затраты на реализацию были мини­мальными, если в сутки выделяется для продажи 5 000 кг муки.

Решение. Составим математическую модель задачи.

Найдем минимум суммарных расходов

При ограничениях:

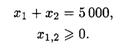
Для расчета модели используем метод множителей Лагранжа. Составим функцию Лагранжа

Найдем частные производные функции F по X1, X2 и λ, приравняем их к нулю, получим систему уравнений

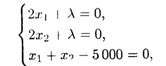
Откуда λ = -5 000, X1 = 2 500, X2 = 2 500, L = 12 500 000 ден. ед.

Давая Х1 значения больше и меньше 2500, находим L и из определения экстремума функции получаем, что L при Х1 = X2 = 2 500 достигает минимума.

Таким образом, для получения минимальных расходов не­обходимо расходовать в сутки через магазин и торговых аген­тов по 2 500 кг муки, при этом расходы на реализацию составят 12 500 000 ден. ед.

< Предыдущая		Следующая >