28.5. Упражнения

Используя графический метод, найти глобальные экстремумы функций.

28.1. L =X1 + 2X2 при ограничениях:

28.2. L = X1 + 3X2 при ограничениях:

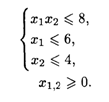
28.3. L = (X1 - 6)2 + (X­2 - 2)2 при ограничениях:

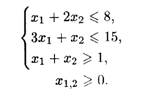
28.4. L = (X1 — 3)2 + (X2 — 4)2 при ограничениях:

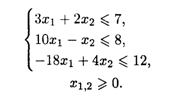
28.5. L = (X1 - 4)2 + (X2 - 3)2 при ограничениях:

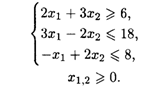
28.6. L = (X1 - 3)2 + (X2 — 2)2 при ограничениях:

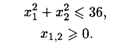
28.7. L = (X1 — 2)2 + (X2 — l)2 при ограничениях:

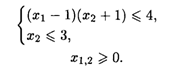
28.8. L = X12 + X22 при ограничениях:

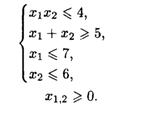
Найти глобальные максимум и минимум дробно-линейных функций.

28.9. L = (2X1 - X2) / (X1 + X2) при ограничениях:

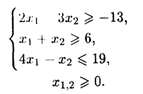
28.10. L = (3X1 - X2)/(X1 + X2) при ограничениях:

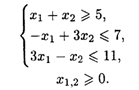
28.11. L = (3X1 + 7X2)/(xL + Х2) при ограничениях:

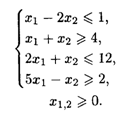
Используя метод множителей Лагранжа, найти точку условно­го экстремума следующих функций.

28.12. L = 2Х1Х3 – х2Х3 при ограничениях:

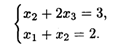
28.13. L = х1Х2 + X2X3, при ограничениях:

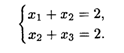
28.14. L = X1X2 + Х2Х3 при ограничениях:

28.15. L = 2X1 — X2 + х3 при ограничениях:

28.16. Фирма реализует автомобили двумя способами: через розничную и оптовую торговлю. При реализации Х1 автомоби­лей в розницу расходы на реализацию составляют 4X1 + Х12 р., а при продаже X2 автомобилей оптом — Х22 р.

Найти оптимальный способ реализации автомобилей, ми­нимизирующий суммарные расходы, если общее число пред­назначенных для продажи автомобилей составляет 200 шт.

< Предыдущая		Следующая >