28.4.1. Метод множителей Лагранжа. Постановка задачи
Дана задача нелинейного программирования
![]()
При ограничениях:
![]()
Предположим, что функции F(X1, Х2,..., xп) и Gi(X1, X2,..., Xп) непрерывны вместе со своими первыми частными производными.
Ограничения заданы в виде уравнений, поэтому для решения задачи воспользуемся методом отыскания условного экстремума функции нескольких переменных.
Для решения задачи составляется функция Лагранжа
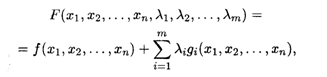
Где λI — множители Лагранжа.
Затем определяются частные производные:
![]()
Приравняв к нулю частные производные, получим систему
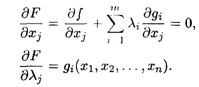
Решая систему, получим множество точек, в которых целевая функция L может иметь экстремальные значения. Следует отметить, что условия рассмотренной системы являются необходимыми, но недостаточными. Поэтому не всякое полученное решение определяет точку экстремума целевой функции. Применение метода бывает оправданным, когда заранее предполагается существование глобального экстремума, совпадающего с единственным локальным максимумом или минимумом целевой функции.
Пример 8. Найти точку условного экстремума функции
![]()
При ограничениях:
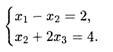
Решение. Составим функцию Лагранжа
![]()
Найдем частные производные функции Лагранжа по переменным X1, X2, X3, λ1, λ2. Приравняв к нулю полученные выражения, решим систему
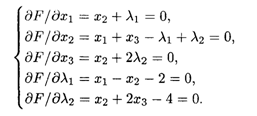
Откуда λ1 = -X2, λ2 = - X2/2, Х1 = -2, X2 = -4, X3 = 4, L = -8.
Определим характер экстремума, изменяя полученные значения переменных. Измененные значения должны удовлетворять заданной системе ограничений. Возьмем Х1 > -2, например X1 = -1, тогда из системы ограничений получим Х2 = -3, X3 = 7/2, L = -15/2. Возьмем Х1 < -2, например Х1 = -3, тогда получим Х2 = -5, X3 = 9/2, L = -15/2. Следовательно, L = -8 — минимальное значение функции.
Ответ. Точка экстремума Х1 = -2, X2 = -4, X3 = 4, при этом максимальное значение функции L = -8.
| < Предыдущая | Следующая > |
|---|