28.3.4. Сведение экономико-математической модели дробно-линейного программирования к задаче линейного программирования

Задачу дробно-линейного программирования можно свести к задаче линейного программирования и решить симплексным методом.

Обозначим

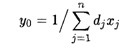
При условии

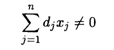
И введем новые переменные УJ = Y0Xj.

Тогда задача примет вид

При ограничениях:

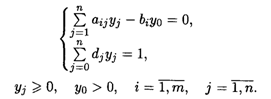
После нахождения оптимального решения полученной зада­чи, используя вышеуказанные соотношения, найдем оптималь­ное решение исходной задачи дробно-линейного программиро­вания.

Пример 7. Дана задача дробно-линейного программирования

При ограничениях:

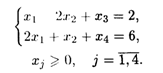
Решение. Обозначим: X1 + 2X2 + 1 = 1/У0, Y0 > 0, тогда L = 2X1Y0 - X2Y0.

Обозначим: X1Y0 = Y1, Х2У0 = у2, х3У0 = У3, Х4У0 = y4.

Преобразуем систему ограничений, умножив обе части всех ограничений на У0, и перейдем к переменным У0, Y1, Y2, Y3, Y4. Задача примет вид

При ограничениях:

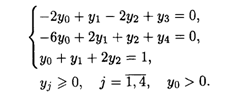
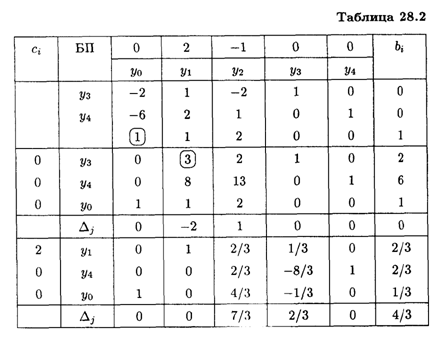
Получили задачу линейного программирования, решаем ее симплексным методом (табл. 28.2).

Получим

Тогда

Ответ: Опт = (2, 0, 0, 2), LMax = 4/3.

< Предыдущая		Следующая >