28.3.3. Применение дробно-линейного программирования для определения себестоимости изделий
Рассмотрим использование дробно-линейного программирования для нахождении себестоимости изделий.
Пример 6. Для производства двух видов изделий А и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в табл. 28.1
Оборудование I и III типов предприятие может использовать не более 26 и 39 ч соответственно, оборудование II типа целесообразно использовать не менее 4 ч.
Определить, сколько изделий каждого вида следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной.

Решение. Составим математическую модель задачи. Пусть X1 — количество изделий вида А, которое следует изготовить предприятию, X2 — количество изделий вида В. Общие затраты на их производство составят (2Х1 + 3X2) тыс. р., а средняя себестоимость одного изделия будет равна
![]()
Математическая модель задачи примет вид
![]()
при ограничениях:
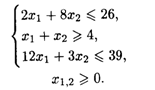
ΔАВС — область допустимых решений (рис. 28.11).
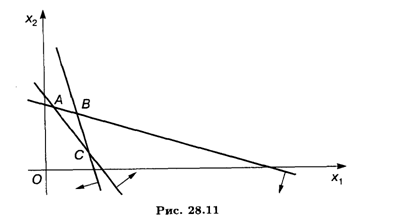
Найдем X2: L = (2X1 + 3X2) / (X1 + X2), 2X1 + 3Х2 = Lx1 + Lx2, X2 (3 - L) = X1 (L - 2),
![]()
Угловой коэффициент прямой равен K = (L - 2)/(3 — L), Тогда
![]()
Так как Dk/DL > 0, то функция K = (L - 2)/(3 - L) возрастает. Это соответствует вращению прямой против часовой стрелки. Следовательно, в точке С (рис. 28.11) целевая функция будет иметь наименьшее значение (глобальный минимум).
Найдем координаты точки С. Решая систему
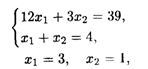
Получим С (3, 1), ![]() Опт = (3, 1), L = 9/4.
Опт = (3, 1), L = 9/4.
Следовательно, предприятию следует выпускать 3 изделия вида А и 1 изделие вида В. При этом средняя себестоимость одного изделия будет минимальной и равной 2,25 тыс. р.
| < Предыдущая | Следующая > |
|---|