28.3.1. Дробно-линейное программирование. Математическая модель задачи

Дробно-линейное программирование относится к нелиней­ному программированию, так как имеет целевую функцию, за­данную в нелинейном виде.

Задача дробно-линейного программирования в общем виде записывается следующим образом:

При ограничениях:

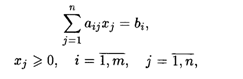
Где Cj, Dj, bi, Aij — постоянные коэффициенты и Djxj ≠ 0.

Рассмотрим задачу дробно-линейного программирования в виде

При ограничениях:

Будем считать, что D1X1 + D2X2 ≠ 0.

Для решения этой задачи найдем область допустимых ре­шений, определяемую ограничениями (28.2). Пусть эта область не является пустым множеством.

Из выражения (28.1) найдем Х2:

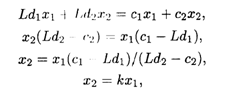
Прямая X2 = Kx1 проходит через начало координат. При некотором фиксированном значении L угловой коэффициент K Прямой тоже фиксирован и прямая займет определенное поло­жение. При изменении значений L прямая Х2 = Kx1 будет по­ворачиваться вокруг начала координат (рис. 28.6).

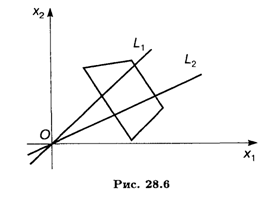
Установим, как будет вести себя угловой коэффициент K При монотонном возрастании L. Найдем производную от K по L:

Знаменатель производной всегда положителен, а числитель от L не зависит. Следовательно, производная имеет постоян­ный знак и при увеличении L угловой коэффициент будет толь­ко возрастать или только убывать, а прямая будет поворачи­ваться в одну сторону. Если угловой коэффициент прямой име­ет положительное значение, то прямая вращается против ча­совой стрелки, при отрицательном значении K — по часовой стрелке. Установив направление вращения, находим вершину или вершины многогранника, в которых функция принимает max(min) значение, либо устанавливаем неограниченность за­дачи.

При этом возможны следующие случаи.

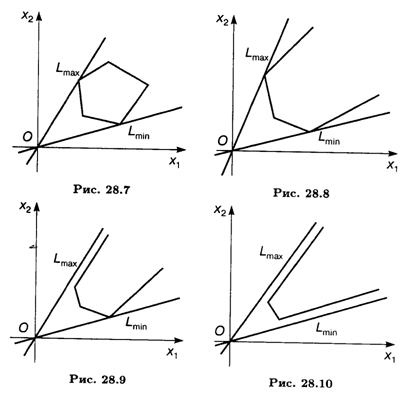
1. Область допустимых решений ограничена, максимум и минимум достигаются в ее угловых точках (рис. 28.7).

2. Область допустимых решений неограничена, однако су­ществуют угловые точки, в которых целевая функ­ция принимает максимальное и минимальное значения (рис. 28.8).

3. Область допустимых решений неограничена, имеется один из экстремумов. Например, минимум достигает­ся в одной из вершин области и имеет так называемый асимптотический максимум (рис. 28.9).

4. Область допустимых решений неограничена. Максимум и минимум являются асимптотическими (рис. 28.10).

< Предыдущая		Следующая >