28.2.3. Задача с нелинейной целевой функцией и нелинейной системой ограничений

Пример 4. Найти глобальные экстремумы функции

При ограничениях:

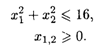
Решение. Областью допустимых решений является ок­ружность с радиусом 4, расположенная в первой четверти (рис. 28.4). Линиями уровня будут окружности с центром в точке O1 (2, l).

Глобальный минимум достигается в точке O1. Глобальный максимум — в точке А (0, 4), при этом

Ответ. Глобальныи минимум, равный нулю, достигается в точке O1 (2, l), глобальный максимум, равный 13, находится в точке А (0, 4).

Пример 5. Найти глобальные экстремумы

При ограничениях:

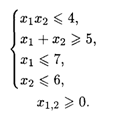
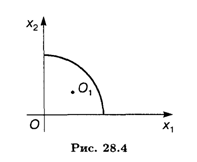
Решение. Область допустимых решений не является вы­пуклой и состоит из двух частей (рис. 28.5). Линиями уровня являются окружности с центром в точке O (0, 0).

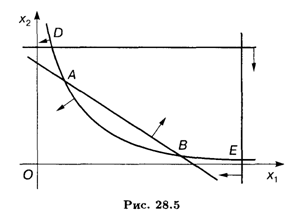
Найдем координаты точек А и В, решая систему

Получим А (1, 4), В (4, 1). В этих точках функция имеет гло­бальные минимумы, равные 17. Найдем координаты точек D И Е, решая системы

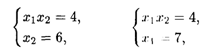
Откуда получаем D (2/3, 6) и L(D) = 328/9, E (7, 4/7) и L(E) = 2417/49.

Ответ. Целевая функция имеет два глобальных миниму­ма, равных 17, в точках А (1, 4) и B (4, 1), глобальный макси­мум, равный 2417/49, достигается в точке E (7, 4/7).

< Предыдущая		Следующая >