28.2.2. Задача с нелинейной целевой функцией и линейной системой ограничений
Пример 2. Найти глобальные экстремумы функции
![]()
При ограничениях:
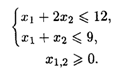
Решение. Область допустимых решений — OABD (рис. 28.2). Линиями уровня будут окружности с центром в
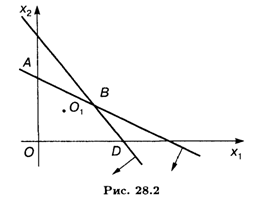
Точке O1. Максимальное значение целевая функция имеет в точке D(9, 0), минимальное — в точке O1 (2, 3). Поэтому
![]()
Ответ. Глобальный максимум, равный 58, достигается в точке D (9, 0), глобальный минимум, равный нулю, — в точке O1 (2, 3).
Пример 3. Найти глобальные экстремумы функции
![]()
При ограничениях:
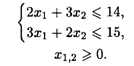
Решение. Область допустимых решений — OABD (рис. 28.3). Линии уровня представляют собой окружности с центром в точке O1 (6, 3). Глобальный максимум находится в точке O (0, 0) как самой удаленной от точки O1. Глобальный минимум расположен в точке Е, находящейся на пересечении прямой 3X1 + 2X2 = 15 и перпендикуляра к этой прямой, проведенного из точки O1.
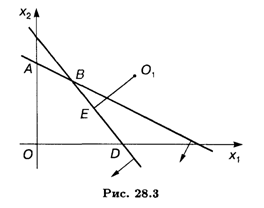
Найдем координаты точки Е: так как угловой коэффициент прямой 3X1 + 2X2 = 15 равен -3/2, то угловой коэффициент перпендикуляра O1Е равен 2/3. Из уравнения прямой, проходящей через данную точку О2 с угловым коэффициентом 2/3, получим
![]()
Решая систему
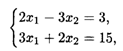
Находим координаты точки Е: х1 = 51/13, X2 = 21/13, при этом L(Е) = 1053/169.
Координаты точки Е можно найти следующим образом: дифференцируя выражение (X1 — 6)2 + (X2 - 3)2 как неявную функцию по X1, получим
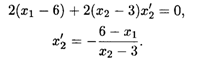
Приравниваем полученное значение к тангенсу угла наклона прямой 3X1 + 2X2 = 15:
![]()
Решаем систему уравнений
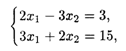
Получим координаты точки Е: х1 = 51/13, X2 = 21/13.
Ответ. Глобальный максимум, равный 52, находится в точке O (0, 0). Глобальный минимум, равный 1053/169, находится в точке E (51/13, 21/13).
| < Предыдущая | Следующая > |
|---|