28.2.1. Графический метод. Задача с линейной целевой функцией и нелинейной системой ограничений

Рассмотрим примеры решения задач нелинейного програм­мирования с двумя переменными, причем их целевые функции и системы ограничений могут быть заданы в линейном и не­линейном виде. Так же как и в задачах линейного программи­рования, они могут быть решены графически.

Пример 1. Найти глобальные экстремумы функции

При ограничениях:

Решение. Область допустимых решений — часть окруж­ности с радиусом 4, которая расположена в первой четверти (рис. 28.1).

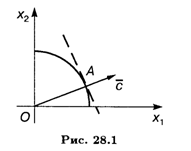
Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2. Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем че­рез точку А прямую, перпендикулярную линии уровня. Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение X2 = 1/2Х1.

Решаем систему

Откуда находим Х1 = 8/5, X2 = 4/5, L = 16/5 + 4/5 = 4.

Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4, — в точке А(8/5, 4/5).

< Предыдущая		Следующая >