23.05. Переход от одного опорного решения к другому

Наличие положительной оценки свободной клетки (ΔIj > 0) при проверке опорного решения на оптимальность свидетель­ствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к друго­му опорному решению. При этом надо перераспределить гру­зы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток — свободной.

Для свободной клетки с ΔIj > 0 строится цикл (цепь, мно­гоугольник), все вершины которого кроме одной находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляют знаки (—) и (+). У вершин со знаком (—) выби­рают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со зна­ком (—). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т. д. до тех пор, пока не получим оптимальное решение.

Рассмотрим переход от одного опорного решения к другому на заданном примере.

Строим цикл для клетки (1,3), имеющей положительную оценку. У вершин цикла ставим знаки (+) и (—) и записываем грузы:

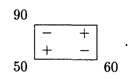
У вершин со знаком (—) выбираем минимальный груз, он равен 60. Его прибавляем к грузам, стоящим у положитель­ных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл:

Новое опорное решение:

Проверим полученное решение на оптимальность. Для это­го запишем его в распределительную таблицу, найдем потен­циалы занятых и оценки свободных клеток (табл. 23.4).

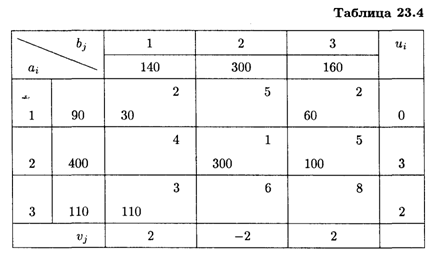
Имеем

Построим цикл для клетки с положительной оценкой Δ21 = 1:

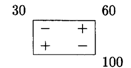
Произведем перераспределение грузов:

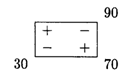
Получим новое решение, которое занесем в табл. 23.5. Прове­рим его на оптимальность.

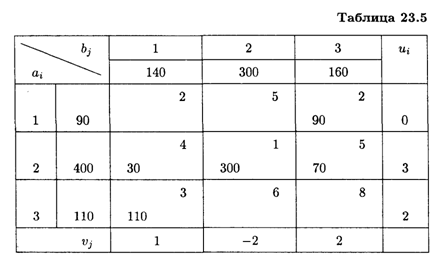
Получим

Все оценки свободных клеток отрицательные, следователь­но, найденное решение оптимальное. Итак,

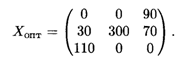
Стоимость транспортных расходов равна

По сравнению с исходным опорным решением транспорт­ные расходы уменьшились на 1610 — 1280 = 330 усл. ед.

< Предыдущая		Следующая >