23.06. Альтернативный оптимум в транспортных задачах

Признаком наличия альтернативного оптимума в транспо­ртной задаче является равенство нулю хотя бы одной из оце­нок свободных переменных в оптимальном решении (XОпт1).Сделав перераспределение грузов относительно клетки, име­ющей ΔIj = 0, получим новое оптимальное решение (ХОпт2), при этом значение целевой функции (транспортных расходов) не изменится. Если одна оценка свободных переменных равна нулю, то оптимальное решение находится в виде

Где 0 ≤ T ≤ 1.

Рассмотрим конкретную задачу, имеющую альтернатив­ный оптимум.

Пример 1. На трех складах имеется мука в количестве 60, 130 и 90 т, которая должна быть в течение месяца доставлена четырем хлебозаводам в количестве: 30, 80, 60, 110 т соответ­ственно.

Составить оптимальный план перевозок, имеющий минимальные транспортные расходы, если стоимость доставки 1 т муки на хлебозаводы задана матрицей

Решение. Составим распределительную таблицу в виде табл. 23.6.

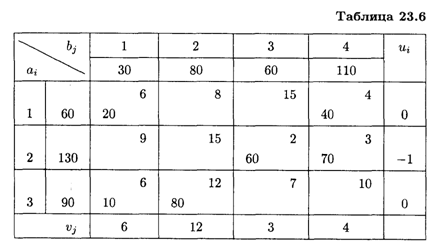
По методу минимального тарифа найдем исходное реше­ние. Определим потенциалы строк и столбцов. Найдем оценки свободных клеток:

Так как Δ12 = 4 > 0, то перераспределим грузы относи­тельно клетки (1,2):

Занесем полученное перераспределение грузов в распреде­лительную таблицу и вычислим потенциалы занятых и оценки свободных клеток (табл. 23.7).

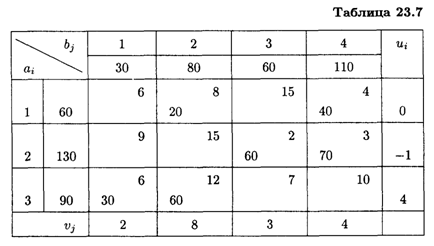
Получим

Так как Δ33 = 0, то задача имеет альтернативный оптимум и одно из решений равно

Стоимость транспортных расходов составляет: L(XОпт1) = 1550 усл. ед.

Произведем перераспределение грузов относительно клетки (3,3):

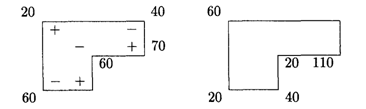
Занесем в распределительную таблицу полученное пере­распределение грузов, вычислим потенциалы занятых и оценки свободных клеток (табл. 23.8):

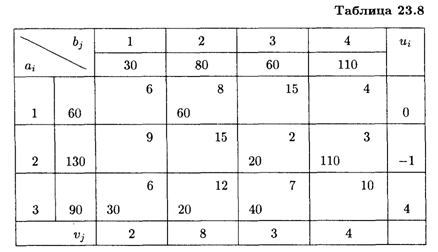
Так как Δ14 = 0, получили еще одно решение:

Стоимость транспортных расходов составит L(ХОпт2) = 1550 усл. ед.

Данная задача имеет два оптимальных решения ХОпт1 и XОпт2, общее решение находится по формуле

Где 0 ≤ T ≤ 1.

Найдем элементы матрицы общего решения:

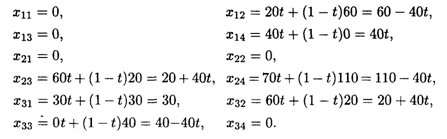
Итак,

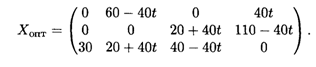
Стоимость транспортных расходов составляет 1550 усл. ед.

< Предыдущая		Следующая >