23.04. Проверка найденного опорного решения на оптимальность
Найденное исходное опорное решение проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение транспортной задачи является оптимальным, то ему соответствует система Т + п действительных чисел Ui и Vj, удовлетворяющих условиям Ui + Vj = Cij для занятых клеток и Ui + vj - сij ≤ 0 для свободных клеток.
Числа Ui и Vj называют Потенциалами. В распределительную таблицу добавляют строку Vj и столбец Ui.
Потенциалы Ui и Vj находят из равенства Ui + vj = Cij, справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например И1 = 0, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал Ui, то Vj = Сij — ui; если известен потенциал Vj, то Ui = Cij – Vj.
Обозначим ΔIj = Ui + vj - cij. Эту оценку называют Оценкой свободных клеток. Если ΔIj ≤ 0, то опорное решение является оптимальным. Если хотя бы одна из оценок ΔIj > 0, то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.
Проверим найденное опорное решение на оптимальность, добавив в распределительную табл. 23.3 столбец Ui и строку Vj.
Полагая U1 = 0, запишем это значение в последнем столбце таблицы.
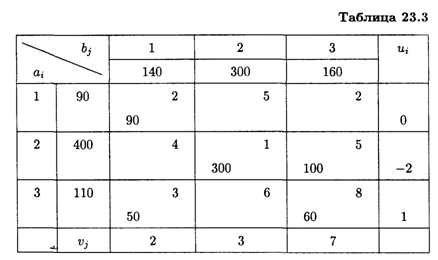
Рассмотрим занятую клетку первой строки, которая расположена в первом столбце (1,1), для нее выполняется условие И1 + V1 = 2, откуда V1 = 2. Это значение запишем в последней строке таблицы. Далее надо рассматривать ту из занятых клеток таблицы, для которой один из потенциалов известен.
Рассмотрим занятую клетку (3,1): И3 + V1 = 3, V1 = 2, откуда И3 = 1.
Для клетки (3,3): И3 + V3 = 8, И3 = 1, V3 = 7.
Для клетки (2,3): И2 + V3 = 5, V3 = 7, И2 = -2.
Для клетки (2,2): U2 + V2 = 1, И2 = -2, V2 = 3.
Найденные значения потенциалов заносим в таблицу.
Вычисляем оценки свободных клеток:
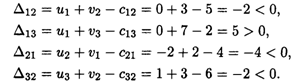
Получили одну оценку Δ13 = 5 > 0, следовательно, исходное опорное решение не является оптимальным и его можно улучшить.
| < Предыдущая | Следующая > |
|---|