21.4. Альтернативный оптимум

При решении задач линейного программирования сим­плексным методом критерием оптимальности является условие ΔJ ≥ 0 для задач на максимум и условие ΔJ < 0 для задач на минимум. Если на каком-то шаге окажется, что хотя бы одна оценка свободной переменной ΔJ = 0, а все остальные ΔJ > 0 для задач на максимум (ΔJ < 0 для задач на минимум), то, приняв в качестве ключевого столбца столбец, где ΔJ = 0, и найдя новое оптимальное решение, заметим, что значение це­левой функции при этом не изменится. Говорят, что в этом случае задача имеет альтернативный оптимум.

Критерием альтернативного оптимума при решении за­дач симплексным методом является равенство нулю хотя бы одной оценки свободной переменной (ΔJ = 0).

Если только одна оценка свободной переменной равна ну­лю, то решение находится по формуле

Где 0 ≤ T ≤ 1.

Если две оценки и более, например S, свободных перемен­ных равны нулю, то оптимальное решение определяется по формуле

В задачах, имеющих альтернативный оптимум, возникает возможность включения в ее модель других критериев эффек­тивности.

Пример. Дана задача линейного программирования

При ограничениях:

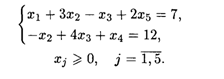
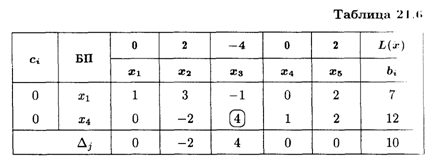
Решение. Составим симплексную таблицу (табл. 21.6).

В индексной строке имеется одна положительная оцен­ка. Полученное решение можно улучшить. Ключевым элемен­том является (4). Составляем симплексную таблицу 2-го шага (табл. 21.7).

Получаем

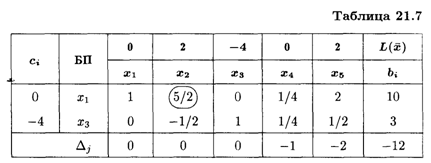
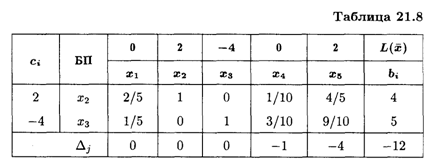
Так как Δ2 = 0, то задача имеет альтернативный оптимум. Найдем еще одно оптимальное решение, введя вместо базисной переменной Х1 свободную переменную Х2 (табл. 21.8).

Получаем

Найдем координаты оптимального решения задачи:

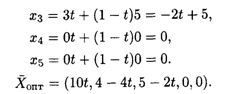
Давая T значения из [0,1], получим различные опт, при кото­рых L() = -12.

< Предыдущая		Следующая >