21.3. Анализ эффективности использования производственного потенциала предприятия

Предприятие располагает тремя производственными ре­сурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными спо­собами. Расход ресурсов за один месяц и общий ресурс при каждом способе производства даны в табл. 21.2 (в усл. ед.).

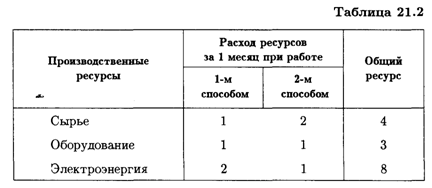
При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором — 4 тыс. изделий.

Сколько месяцев должно работать предприятие каждым из этих способов, чтобы при наличных ресурсах обеспечить мак­симальный выпуск продукции?

Решение. Составим математическую модель задачи. Обо­значим: X1 — время работы предприятия первым способом, X2 — время работы предприятия вторым способом.

Математическая модель имеет вид

При ограничениях:

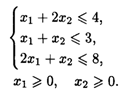
Приведем задачу к каноническому виду:

При ограничениях:

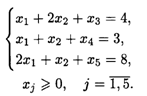
Составляем симплексную таблицу 1-го шага (табл. 21.3).

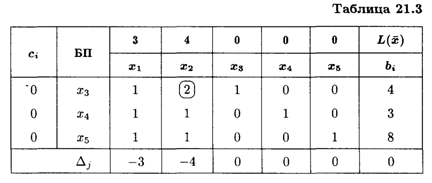
Получим решение:

В индексной строке ΔJ имеются две отрицательные оцен­ки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве ключевого столбца следу­ет принять столбец базисной переменной Х2, а за ключевую строку взять строку переменной X3, где min (4/2,3/l, 8/1) = min (2, 3, 8) = 2.

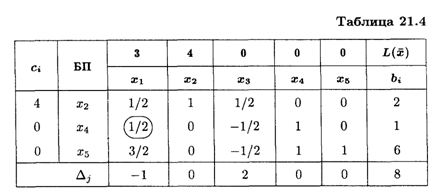
Ключевым элементом является (2). Вводим в столбец ба­зисной переменной Х2, выводим Х3. Составляем симплексную таблицу 2-го шага (табл. 21.4).

Получим

В индексной строке имеется одна отрицательная оценка. Полученное решение можно улучшить. Ключевым элементом является (1/2). Составляем симплексную таблицу 3-го шага (табл. 21.5).

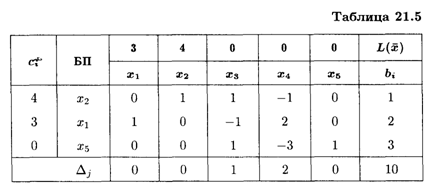
Все оценки свободных переменных ΔJ ≥ 0, следовательно, найденное опорное решение является оптимальным:

Таким образом, по первому способу предприятие должно работать два месяца, по второму — один месяц, при этом мак­симальный выпуск продукции составит 10 тыс. ед.

< Предыдущая		Следующая >