18.3. Система двух случайных величин. Двумерная случайная величина

До сих пор мы рассматривали дискретные случайные ве­личины, которые называют одномерными: их возможные зна­чения определялись одним числом. Кроме одномерных вели­чин рассматривают также величины, возможные значения ко­торых определяются несколькими числами. Двумерную слу­чайную величину обозначают через (X, Y); каждая из величин X и Y называется компонентой (составляющей). Обе величи­ны Х и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Например, при штамповке стальных пластинок их длина и ширина представляют собой двумерную случайную величину.

Определение 1. Законом распределения двумерной случай­ной величины (X, Y) называют множество возможных пар чи­сел (Xi, Yj) и их вероятностей P(Xi, Yj). Двумерную случайную величину можно трактовать как случайную точку А(Х, Y) на координатной плоскости.

Закон распределения двумерной случайной величины обыч­но задается в виде таблицы, в строках которой указаны воз­можные значения Xi случайной величины X, а в столбцах — возможные значения Yj случайной величины Y, на пересече­ниях строк и столбцов указаны соответствующие вероятности Pij. Пусть случайная величина Х может принимать П значе­ний, а случайная величина Y - Т значений. Тогда закон рас­пределения двумерной случайной величины (X, Y) имеет вид

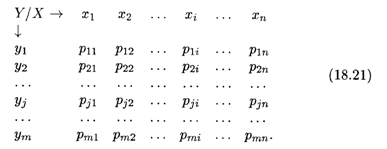
Из этой таблицы можно найти законы распределения каждой из случайных компонент. Например, вероятность того, что слу­чайная величина Х примет значение Хk, равна, согласно тео­реме сложения вероятностей независимых событий,

Иными словами, для нахождения вероятности Р(хk) Нужно просуммировать все Т вероятностей по K-Му столб­цу таблицы (18.21). Аналогично получается вероятность то­го, что случайная величина Y примет возможное значение Уr: Р(уr) получается суммированием всех N вероятностей R-й стро­ки таблицы (18.21) (R = 1, 2, ... ,M). Отсюда следует, что сумма всех вероятностей в законе распределения (18.21) равна единице:

Пример 1. Задано распределение двумерной случайной вели­чины:

Найти распределения Х, Y и Х + Y.

Решение. В нашем случае возможные значения случайной величины X: х1 = 1, Х2 = 2, X3 = 3. Тогда, согласно формуле (18.22), имеем P(X1) = 0,1 + 0,2 = 0,3, P(X2) = 0,15 + 0,22 = 0,37, Р(x3) = 0,12 + 0,21 = 0,33. Отсюда получаем закон распреде­ления X:

Аналогично получаем и для распределения Y: У1 = 1, Y2 = 2; P(Y1) = 0,1 + 0,15 + 0,12 = 0,37, P(Y2) = 0,2 + 0,22 + 0,21 = 0,63;

Теперь найдем распределение X+Y. Возможные значения этой случайной величины: 2, 3, 4 и 5. Соответствующие вероятнос­ти Р(2) = 0,1, Р(3) = 0,15 + 0,2 = 0,35, Р(4) = 0,12 + 0,22 = 0,34, Р(5) = 0,21. Отсюда находим искомое распределение:

В случае системы двух случайных величин используются кроме математических ожиданий и дисперсий еще и другие числовые характеристики, описывающие их взаимосвязь.

< Предыдущая		Следующая >