18.2.5. Начальные и центральные моменты

Определение 5. Начальным моментом порядка K случай­ной величины Х называется математическое ожидание вели­чины ХK:

В частности,

И тогда формула (18.11) для вычисления дисперсии принимает вид

Определение 6. Центральным моментом порядка K случай­ной величины Х называется математическое ожидание K-Й сте­пени отклонения:

В частности, согласно формуле (18.9), μ1 = 0, а дисперсия слу­чайной величины Х является центральным моментом второго порядка:

Соотношения, связывающие начальные и центральные мо­менты, также могут быть легко получены. Приведем их здесь для моментов третьего и четвертого порядков (они наряду с моментами первого и второго порядков широко применяются в статистике):

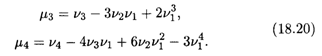
Моменты более высоких порядков применяются крайне редко.

Моменты, рассмотренные в этом разделе, называют Те­оретическими. В отличие от них моменты, вычисляемые по данным наблюдений в математической статистике, называют Эмпирическими.

< Предыдущая		Следующая >